This project as titled explores the golden ratio phenomena, specifically within sunflower seeds growth and how different variants are suboptimal for sunflowers.
INTRODUCTION
“The seed heads of sunflowers optimize the packing of seeds by growing florets in a spiraling pattern connected to the golden ratio and Fibonacci sequence”. Ask Nature.
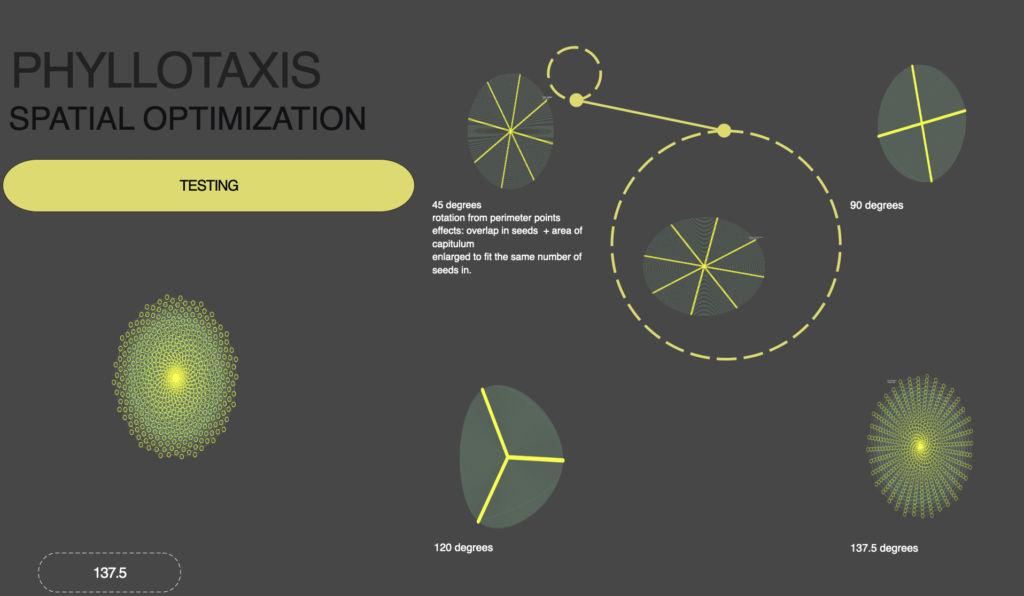
In nature, the growth patterns of plants exhibit a remarkable alignment with mathematical principles, particularly through the adoption of the golden angle, approximately 137.5 degrees. This strategic angle ensures efficient space utilization and optimal exposure, preventing overlap among growing parts. It is deeply connected to the golden ratio, 1.618, a key figure in the Fibonacci sequence, where each number is the sum of the two preceding ones. This sequence is evident in various natural formations, from flower heads to nautilus shells, demonstrating a universal pattern of development. The golden ratio and angle exemplify the intricate link between mathematics and natural growth, highlighting a fundamental computational logic in the natural world.
GOLDEN RATIO
Golden Ratio and Fibonacci Numbers:
- The Fibonacci sequence is a series where each number is the sum of the two preceding ones (e.g., 0, 1, 1, 2, 3, 5, 8, 13, …).
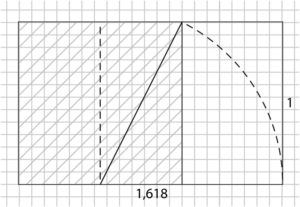
- As the sequence progresses, the ratio of consecutive Fibonacci numbers approximates the golden ratio (1.618…).
- This ratio represents an ideal proportion in various natural and human-made structures, embodying aesthetic and functional harmony.
Golden Ratio in Sunflowers:
- Sunflower seeds are arranged in spirals that follow the Fibonacci sequence, optimizing space and reducing shadowing among seeds.
- The angle between successive seeds in a sunflower head approximates the golden angle (about 137.5 degrees), which is derived from the golden ratio.
- This arrangement allows for efficient packing and maximal exposure to sunlight, demonstrating the golden ratio’s role in natural growth patterns.
Sunflowers and the Golden Ratio (phyllotaxis)
- The word “Phyllotaxis” originating from the Greek words for ‘leaf’ and ‘arrangement’ is the name given to the pattern in sunflower seeds. This is also visible in other natural forms eg: pine cones or pineapple.
- Spiral phyllotaxis uses an angle of 137.5 degrees to position each new seed formed. This proves to be the perfect angle by which to tightly pack in as many seeds, so creating this pattern

SUNFLOWER: Capitulum components
- Capitulum: Sunflower Head characterized by a dense cluster of small flowers (florets) arranged on a flat or convex base
- Ray Florets: florets that form on the perimeter of the sunflower head, known for their bright yellow color. They are sterile, do not produce pollen or seeds, and serve primarily to attract pollinators with their vivid appearance.
- Disk Florets: small, tubular flowers located at the center of a sunflower head. They are fertile, producing both pollen and seeds, and are closely packed in a spiral pattern.

- if you count these spirals, the total number tends to be a Fibonacci number. For instance, you might see 34 spirals in one direction and 55 in the other, both of which are Fibonacci numbers.
- The reason behind this lies in growth efficiency

PHYLLOTAXIS
PSEUDO CODE
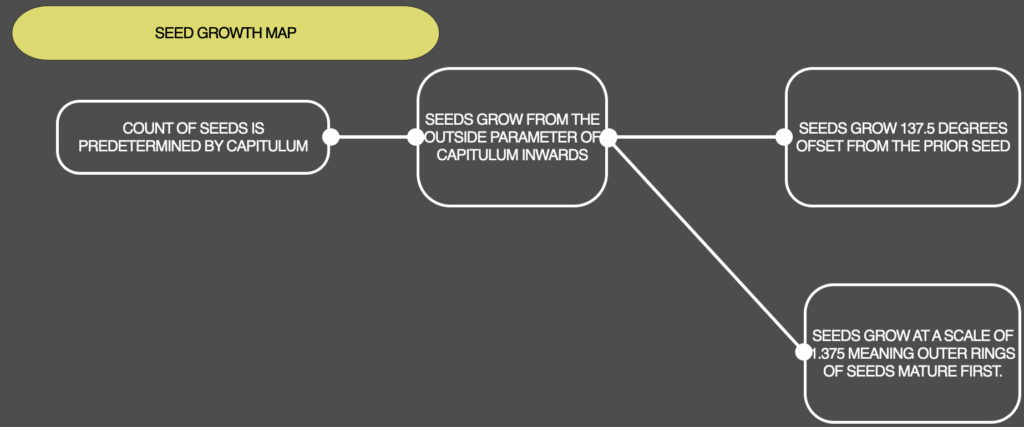
Seeds Placement
- Number of seeds counter series.
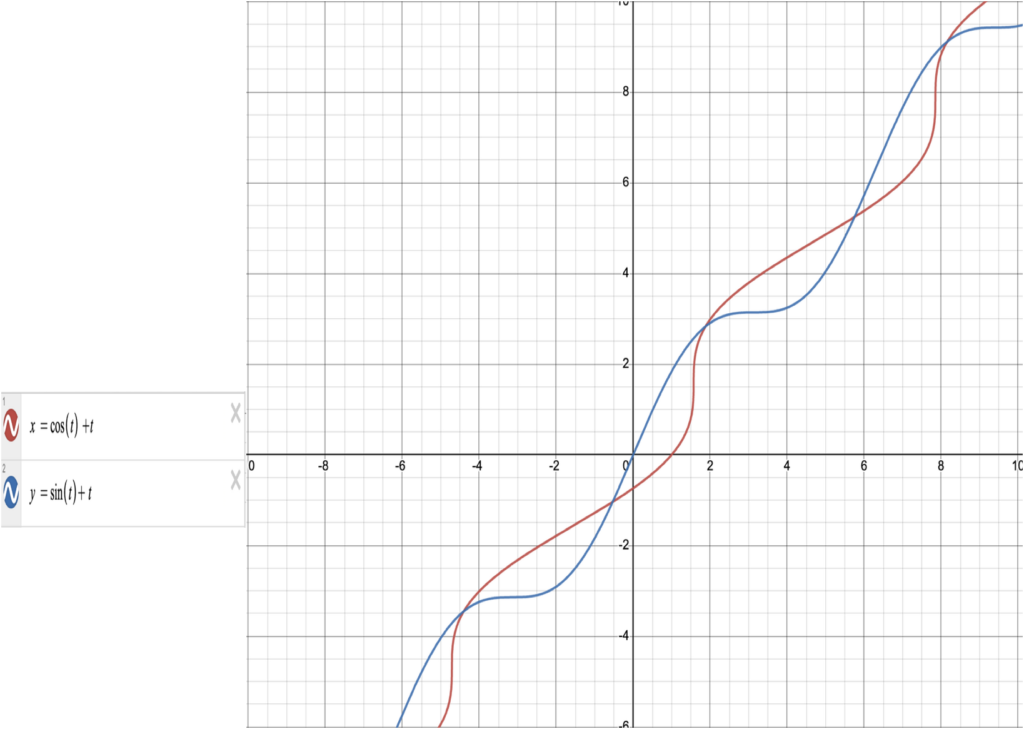
- Expression component for x = cos(t) + t
- Expression component for y = sin(t) + t
- Construct component on the plane.
when placed within a capitulum each point is placed at the intersection of the graph displayed.
Simulating Growth
- Number of seeds counter series.
- Multiplication component by 137.5
- Convert to radians component
- Anemone for loop through each seed placement and growth .