Introduction
The objective of this Data Science project is to investigate the possible evolution that the value of a chess piece may experience when they’re allowed to move on a board of higher dimensions. The project will analyse the movement of the chess pieces beyond the 2d plane and onto the 3d cube, 4d hypercube on another nth dimensional shape.
Methodology
In order to be able to compare pieces moving in different dimension game boards it’s crucial to specify a way to give value to a piece. Defining what constitutes the value of a chess piece in the game and how that plays into the hierarchy of the pieces has never been a trivial matter. In chess the standard value that is given to each piece is as follows:
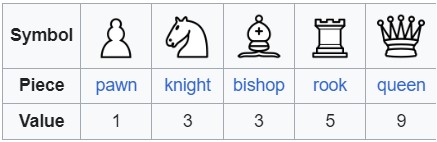
Most well known and popular valuations derived from this standar, nevertheless due to the complexity of the game, these values aren’t assigned through an analytical approach but rather an empirical one. Since the most prominent effect of using higher dimensional game boards is to give new degrees of freedom to the pieces movement, this project evaluates the pieces based on their reach and flexibility of movement.
For the purpose of studying the movement of the chess pieces in 3, 4 or even 5 dimensions, it is necessary to abstract the movement into a more general set of rules that can translate to the new axis of movement. Visualizing the abstraction also allows to get an initial understanding about how the movement changes in higher dimensions. There are many ways in which the current movement of the chess pieces can be abstracted, and in term, these different ways lead to different ways for each piece to explore the space, the project chooses to use the following abstractions:

 Knight
Knight
The default movement of the knight piece on a 2d chessboard is an “L” shaped movement, and the abstraction that is constructed from that movement is the following:
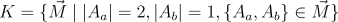
All possible movements that a knight can make on an Nth dimensional board are those where the piece moves 2 cells on an initial axis Aa and 1 cell in a second axis Ab.
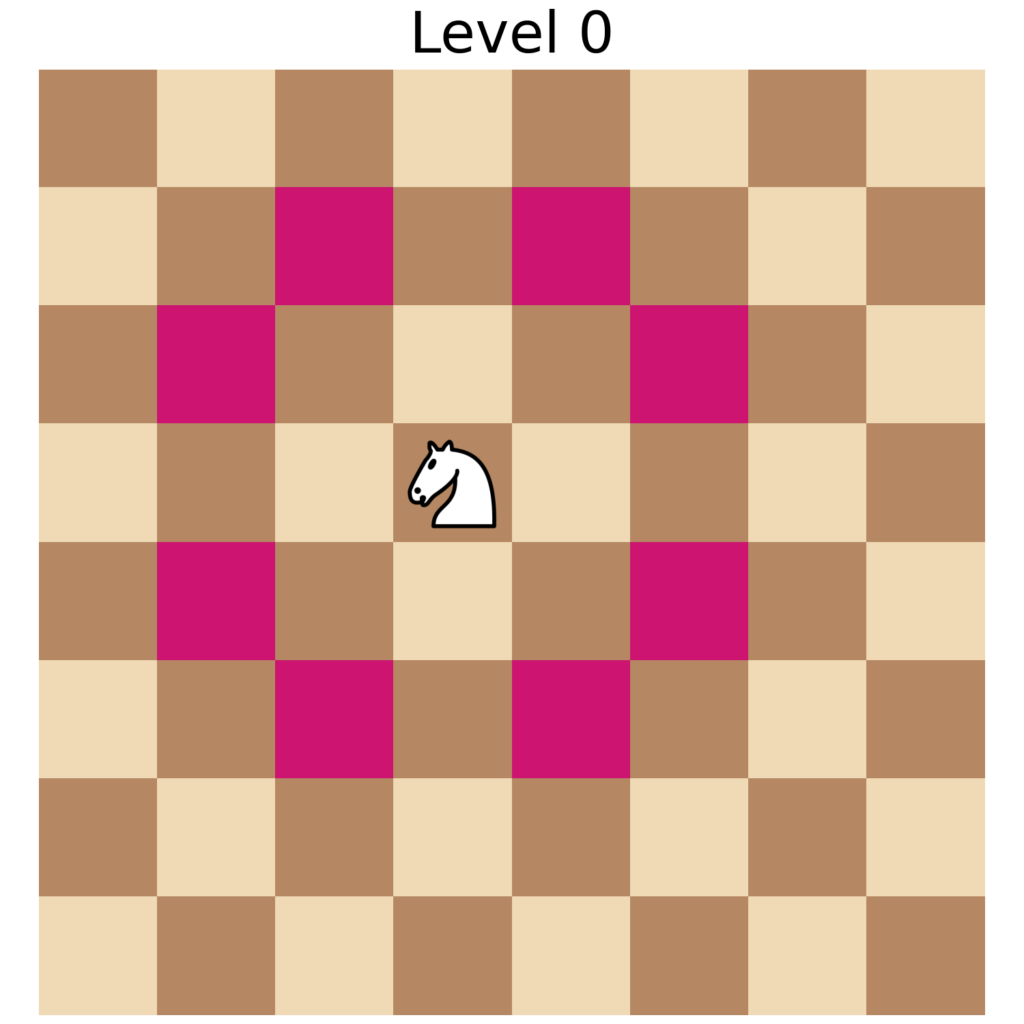


The visualization of the knights movement in 2D, 3D, and 4D shows that the piece pattern of movement acts similar to a sphere or circle, where the cells that the knight can reach are those that are a certain radius from the piece current position.
 Bishop
Bishop
The bishop moves in 45° diagonals throughout the board, without a limit to the distance it can travel. One possible abstraction to these rules would be that it can move any amount of cells desired as long as it moves an equal amount in each dimension, but that would lead in higher dimensions to an uncharacteristic movement for the bishop since it would allow it to move to both dark and light coloured cells. Due to this issue the abstraction constructed is slightly different:
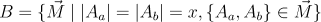
The movements that a bishop is allow to take on a chessboard of dimension n, are those where the piece moves any equal ammount of cells in 2 different axis.


This abstraction of the bishop movement mantain the characteristic limitation that the bishop has that makes it only possible for it to move to cells of the same color.
 Rook
Rook
The movement of the rook is one of the most simple ones. It can move in any orthogonal direction any amount of cells it requires. This type of movement translates very easily to a higher dimension. The abstraction then is:
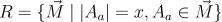
All the available movements for the rook in any dimensions, are those that consist of moving any amount of cells in a single axis.
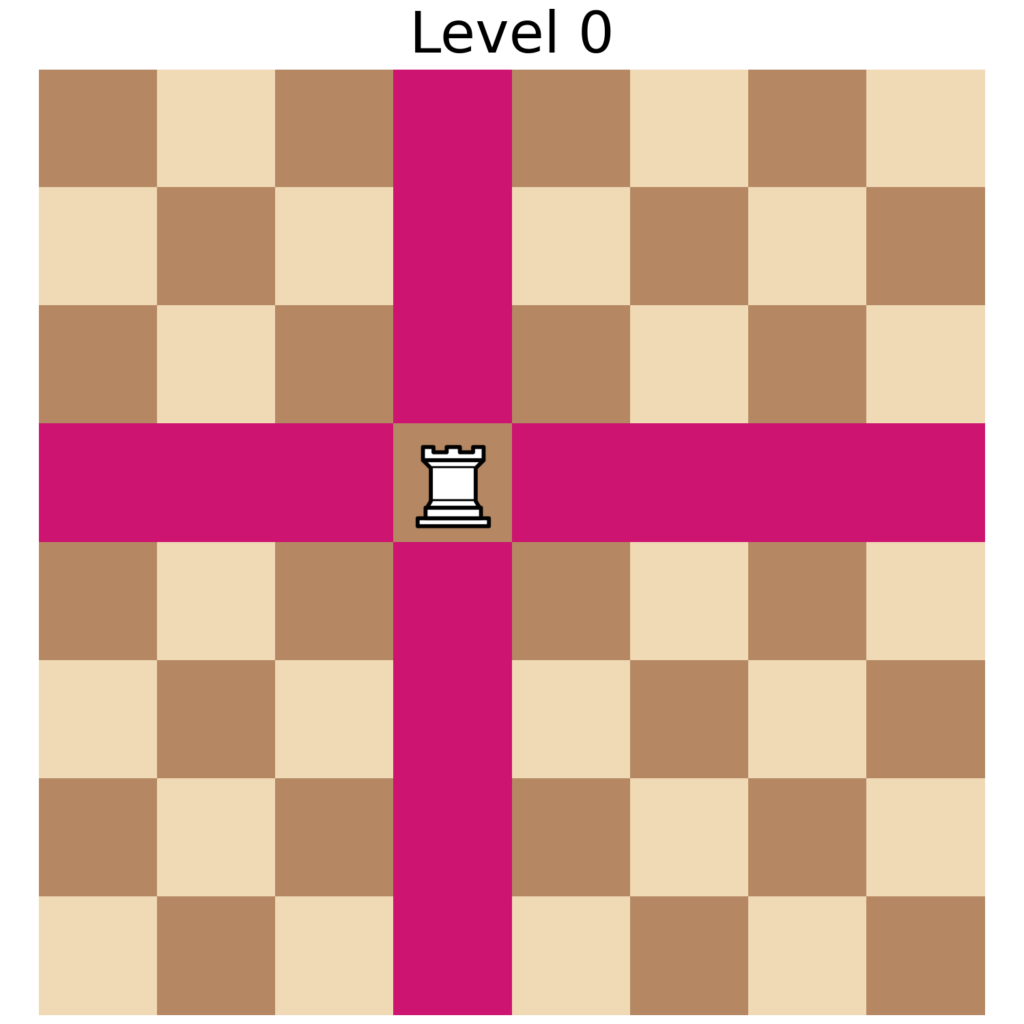


Plotting the movement of the rook in higher dimensions reveals a surprising fact, which is that the higher the dimension of the chessboard the hardest it becomes for the rook to reach most of the 2D sections of the board. We can see in the 3D and even more clearly in the 4D boards, that outside the initial 2D section where the rook is positioned, any other section that it can reach, can only reach a single cell.
 Queen
Queen
The way the queen moves is an amalgamation of the movement of the rook and the bishop, similarly unrestricted in the amount of cells it can move at a time. Therefore the abstraction to bigger dimensions is also constructed as the union of the Bishop and Rook:
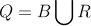
This abstraction means that the queen can move through the Nth dimensional board, by moving any amount of cells in a single axis, or moving any amount of cells equally in two axes.


Unsurprisingly the queen still has the most reaching set of possible moves on a higher dimensional board, but it becomes clear that the higher the dimension the least amount of cells it can reach in a single move
Analysis
The technique with which the piece’s movement is measured is by programmatically creating a mask layer, based on each piece’s abstraction of movement, in the form of a matrix that stores the types of movement each piece can take. The matrix is then overlaid with the current board state highlighting the cells the piece can move towards. The mask matrix is larger than the board, approximately 2 times larger, in order to highlight all the cells a piece can reach regardless of its position on the board. After being overlaid the mask is then clipped which results on the board with the new possible positions the piece can have after the one turn, being highlighted. This process is iterated x amount of times to get the possible movement after x amount of turns. From this technique a heatmap is constructed to visualize the reach at each movement step, and later a line graph is plotted to quantify and compare the reach of each movement step.
 Knight
Knight
Heatmap
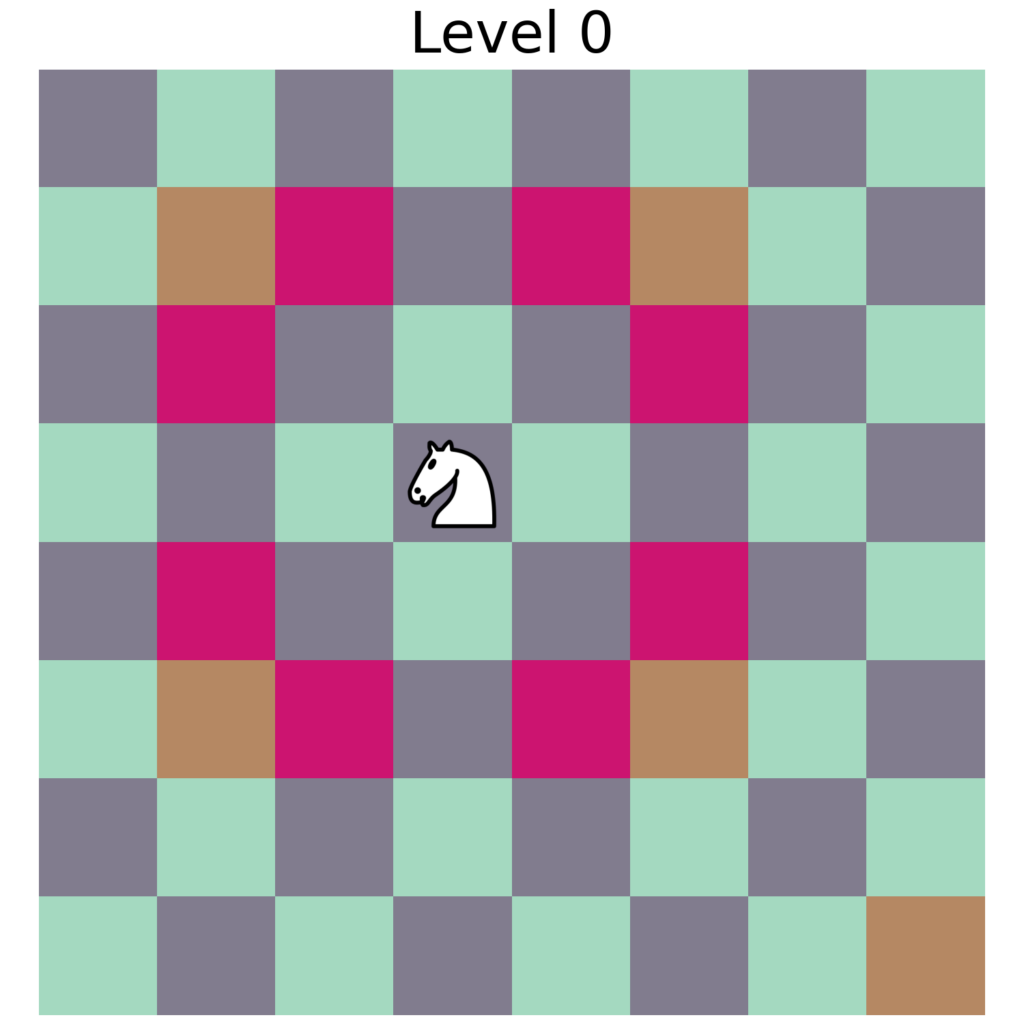

The heatmap analysis of the knights movement reinforces the intuitions that the visualization of the movement abstraction provided. The knight moves in a pattern similar to a circle/sphere where it moves based on a radius from the initial position. Nevertheless, this analysis offers a new insight it seems that, and it’s more clear in the cells that are the furthest away from the initial position, depending if the turn is odd or even the knight can only move to dark or light cells.
Quantities
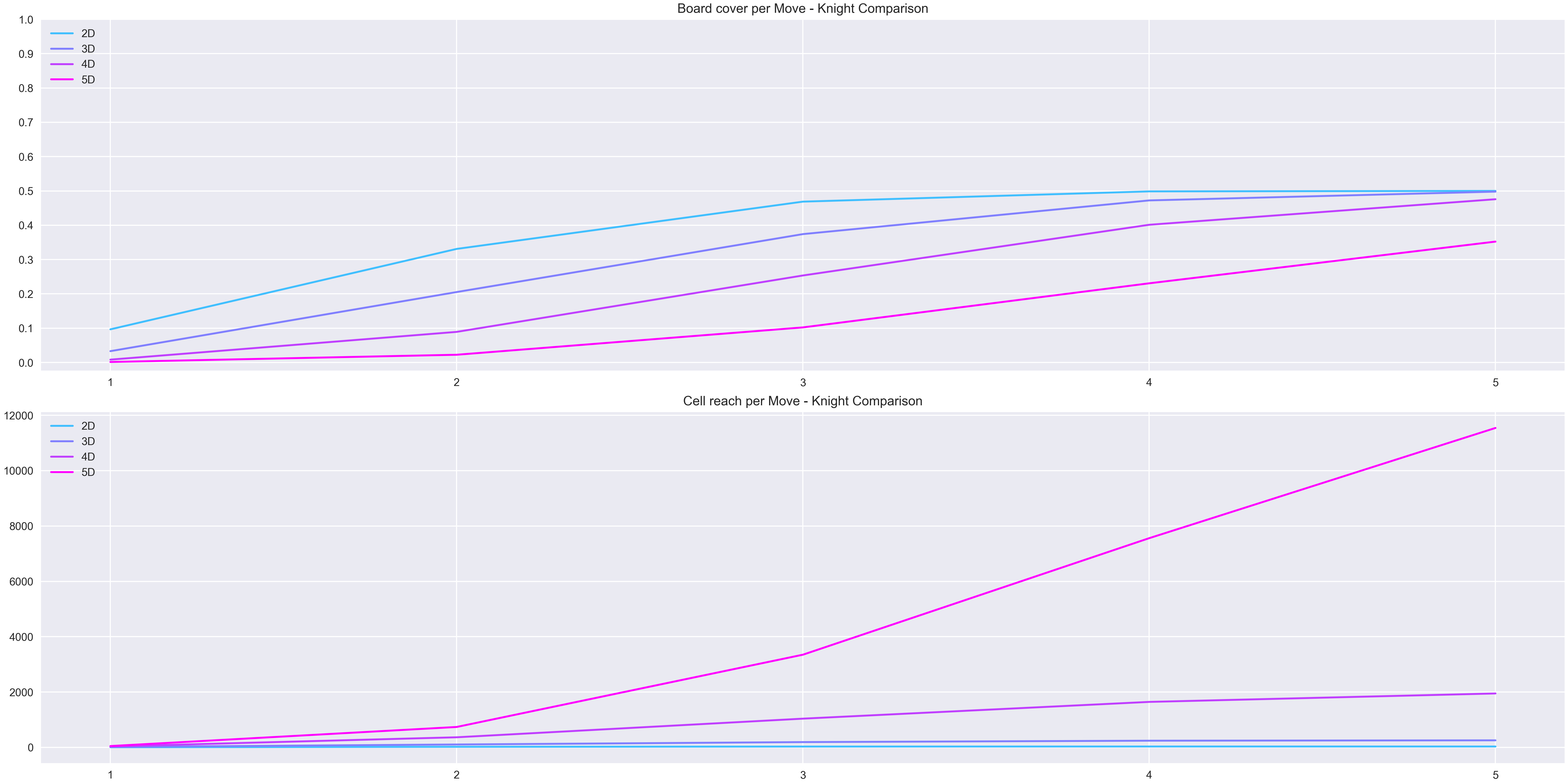
When quantifying the movement of the knight and comparing them on the different Nth dimensional chessboard we can see that the change in reach for the piece changes quite steadily. In all studied dimensions the knight begins with a reach of around 10% of the total cells, and by the 5th movement it the night can reach 50% percent of the cells, except for in the 5D case where it reaches 35%. In terms of total cells that are reachable it is curious that even though logically in higher dimension the total quantities of cells that are reachable grows, the jump to 5D is the one with the most growth.
 Bishop
Bishop
Heatmap



The heatmap of the movement of the bishop in different dimensions, shows how the maximum reach that the bishop can have is 50% of all cells. This is due to only being able to move through either dark or light cells.
Quantities
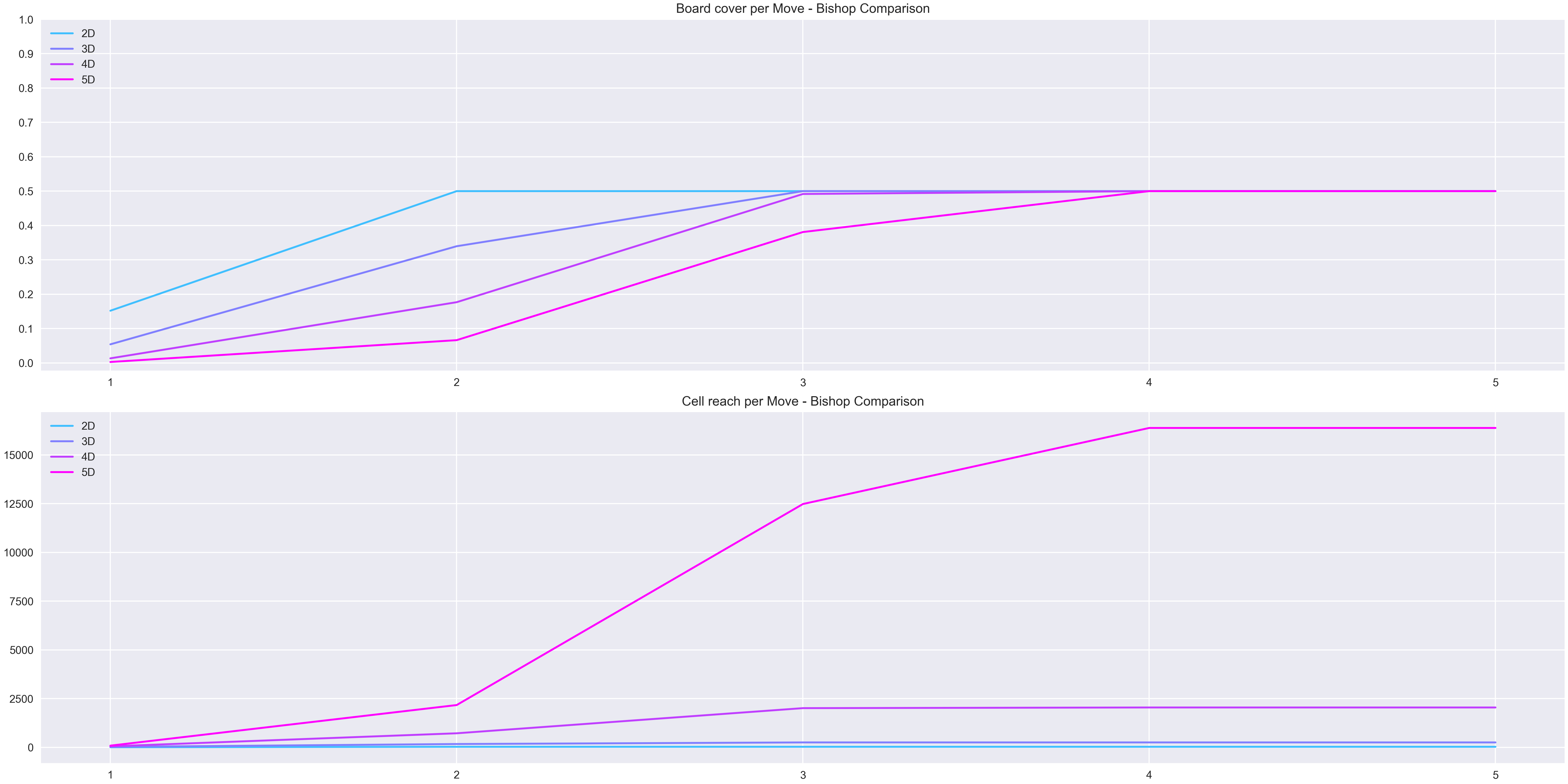
Quantifying the bishop movement and plotting the numbers again demonstrates that the maximum reach for the bishop, regardless of the dimension of the chessboard, is 50% of the cells because of its rules of movement. What’s interesting is that the dimension of the board determines how many movements it needs to get to the 50%, for 2D board it’s reached by the second movement, for 3D & 4D it needs one extra movement, and in the case of 5D it needs yet another step. Like with the knight, the total quantity of cells that the bishop can reach per movement grows with the dimension, and a big jump appears on the 5th dimension.
 Rook
Rook
Heatmap
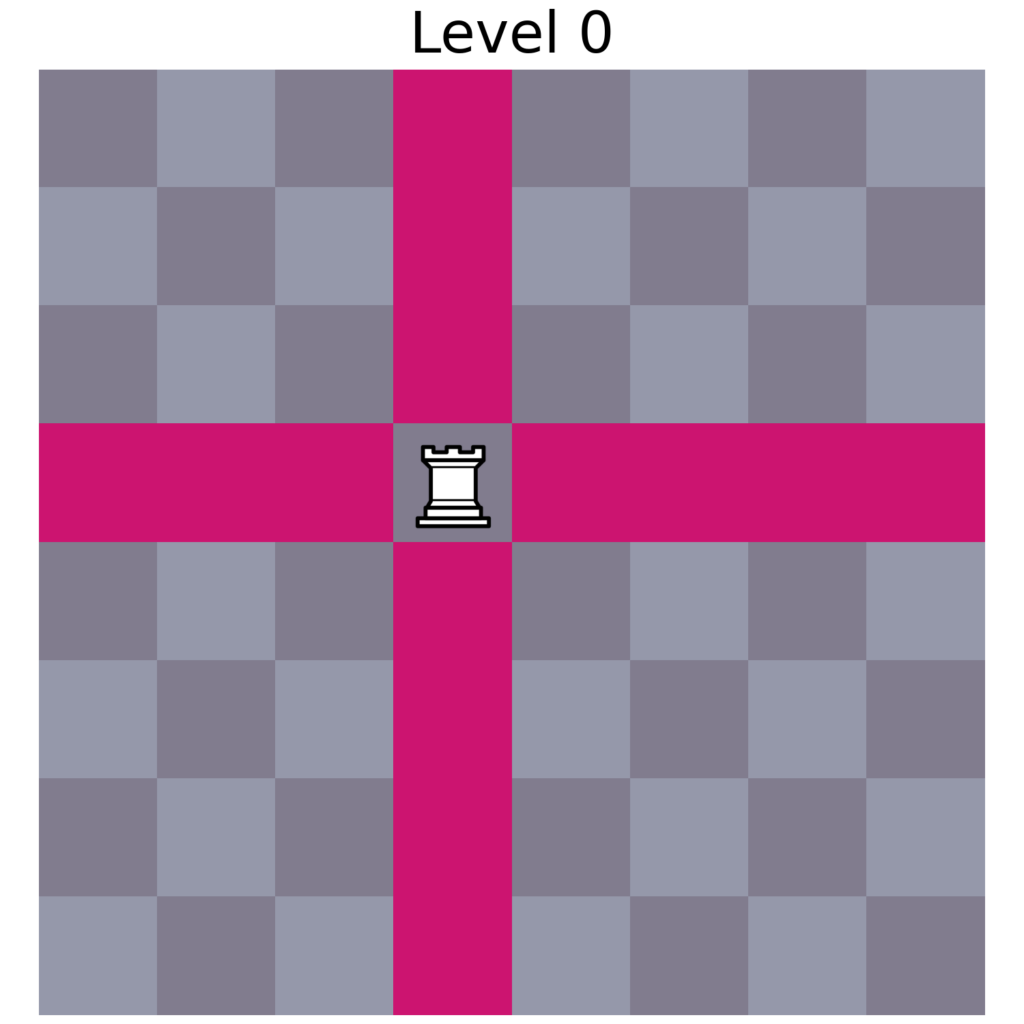


The visualization of the movement of the rook demonstrates how its movement that relies on moving on an orthogonal axis, becomes quite limiting in higher dimensions. The piece’s orthogonal movement is so restrictive that it clearly reflects on the visualization of its movement.
Quantities
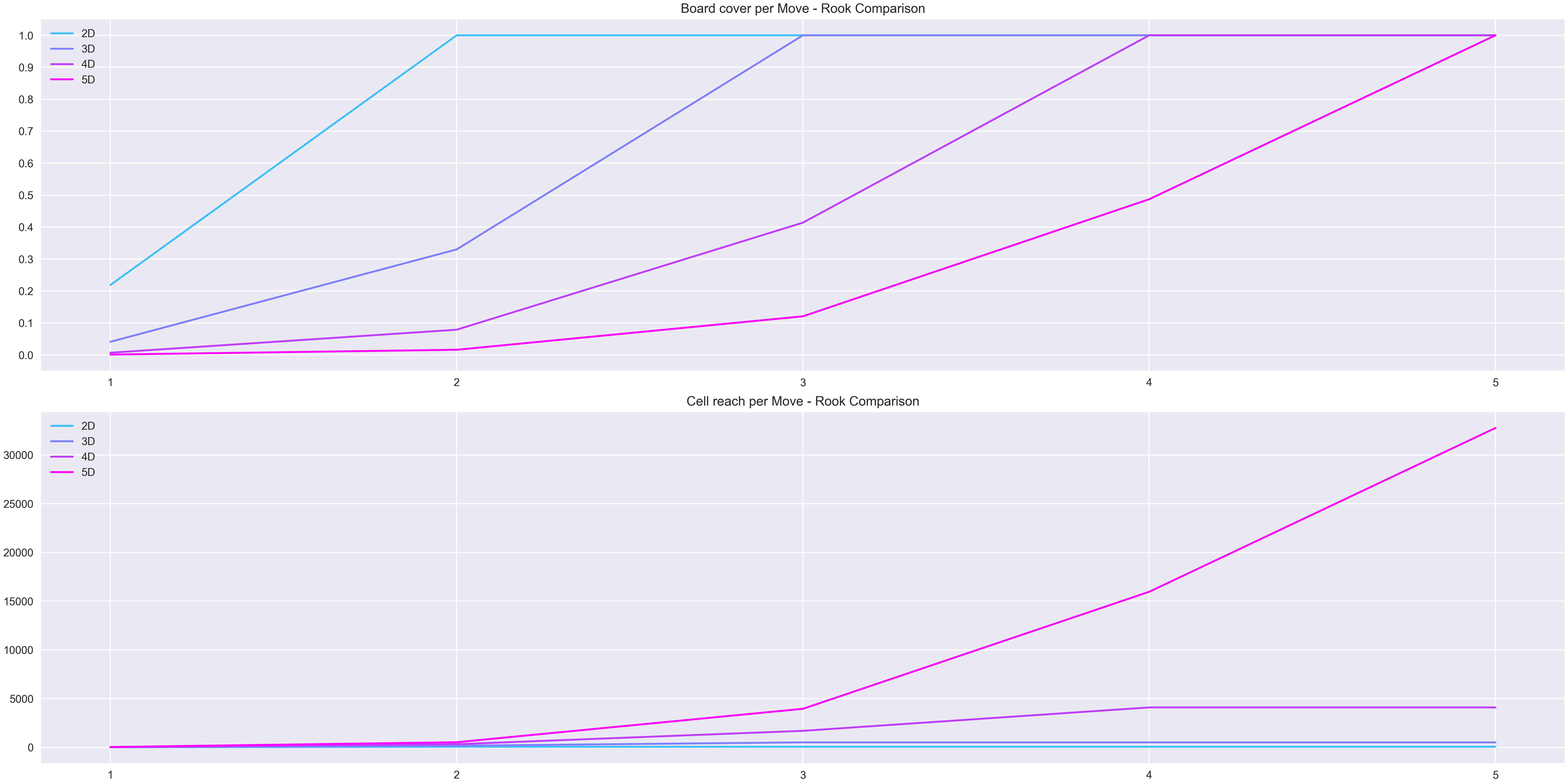
The rooks movement when plot shows a strong pattern: for each jump to a higher dimension it takes one extra move to reach its maximum reach (which is 100% of the cells). The analysis of the total quantity of cells that it can reach, similarly like with the previous pieces has a big growth when in the 5th dimension, but in contrast with the other pieces where that growth based on the movement grew similar to a sigmoid function, with the rook the curve its closer to an exponential function.
 Queen
Queen
Heatmap


The reach of the queen as shown by the heatmap clearly illustrates the dominance of the piece, even though the higher the dimension the harder it’s for the piece to reach all parts of the board it is apparent that its freedom of movement can keep up the reach for longer.
Quantities
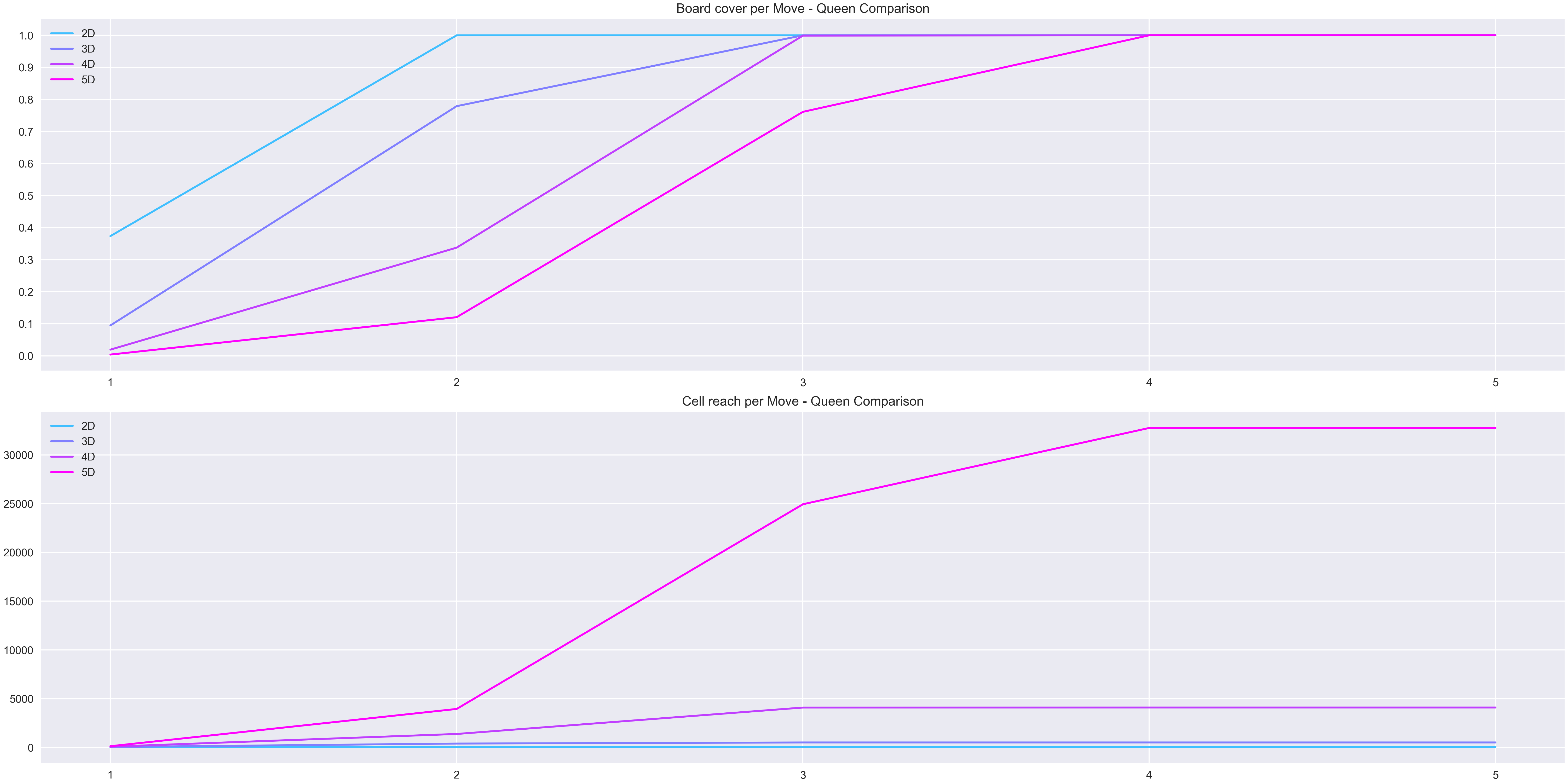
The quantification of the queens movement reflects the previous intuitions about it. The fact that their movement is a combination of the rook and the bishop gives it a freedom that translates to being able to reach 100% of the cell with little moves.
Conclusion
Lastly, line graphs comparing the reach percentage of the total cells and the reach total quantity for each dimension are plotted to depict the change in the hierarchy of the pieces on higher dimensions.
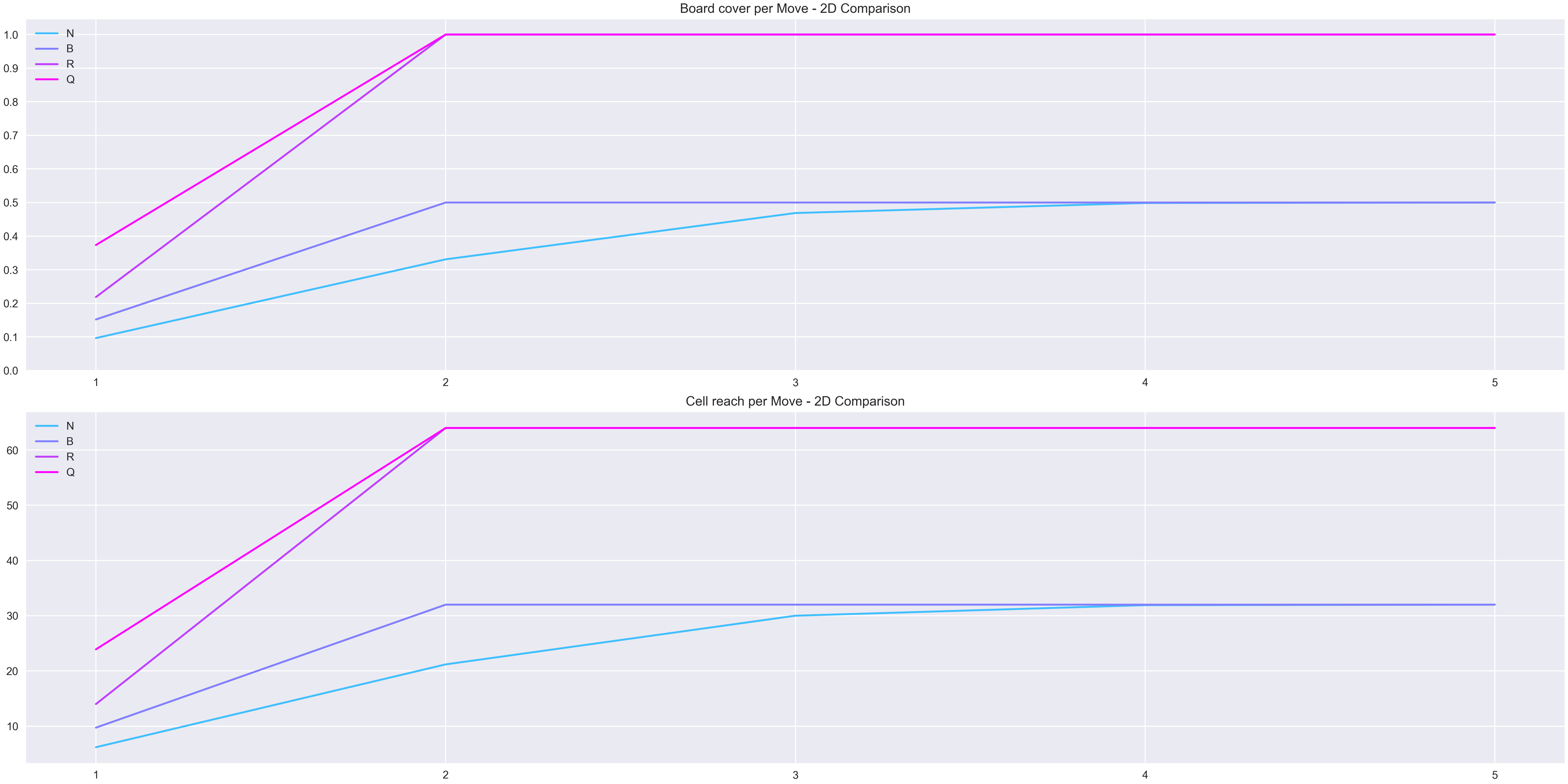
For the 2D board the standard valuation is reflected on their movement. From best to worst: queen, rook, bishop, knight.
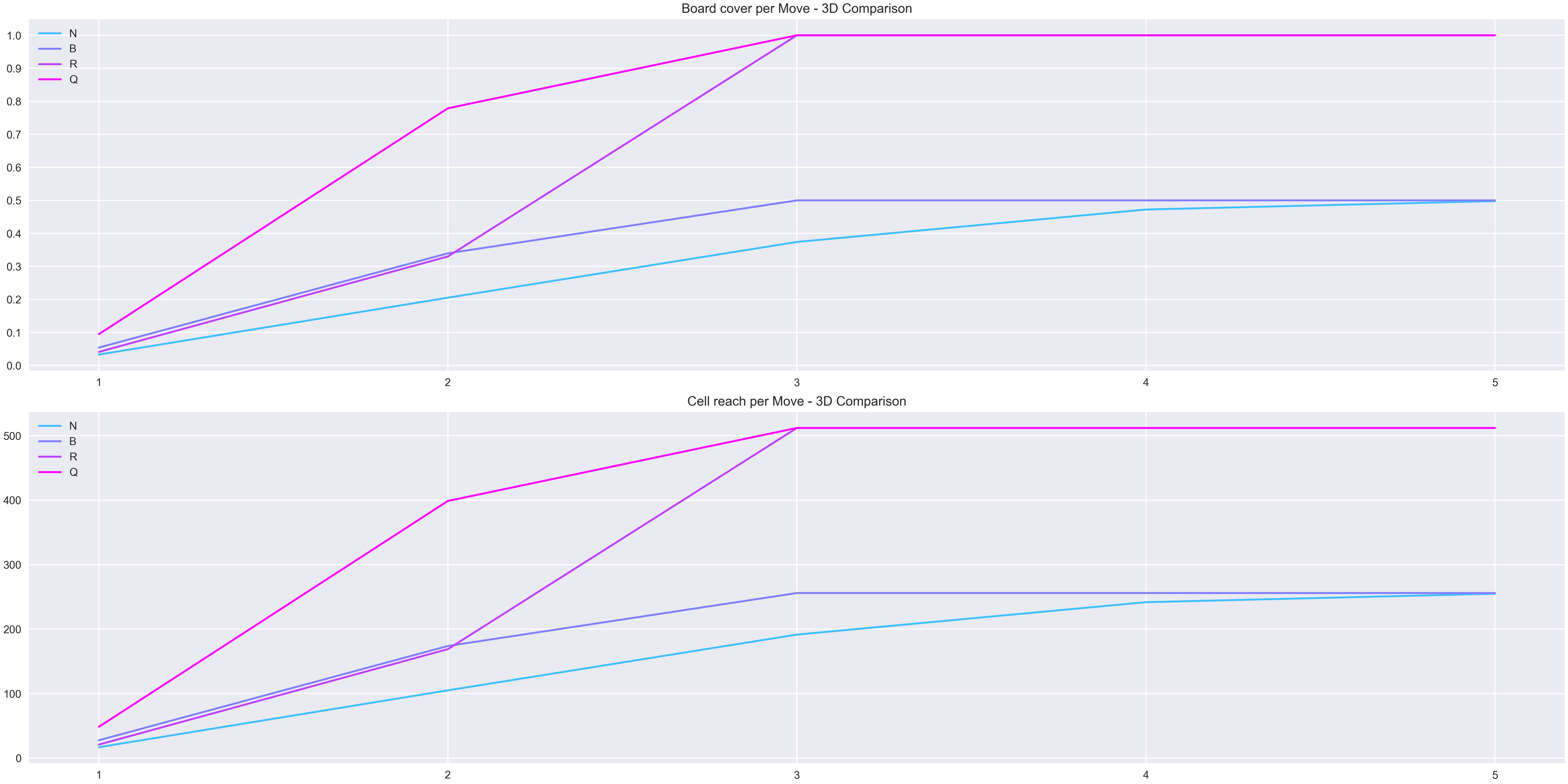
In the 3D dimension, the rook loses advantage compared to the bishop in the 2 move, which makes it a slightly less flexible piece when only two turns are played. But on the 3rd move it regains the advantage.
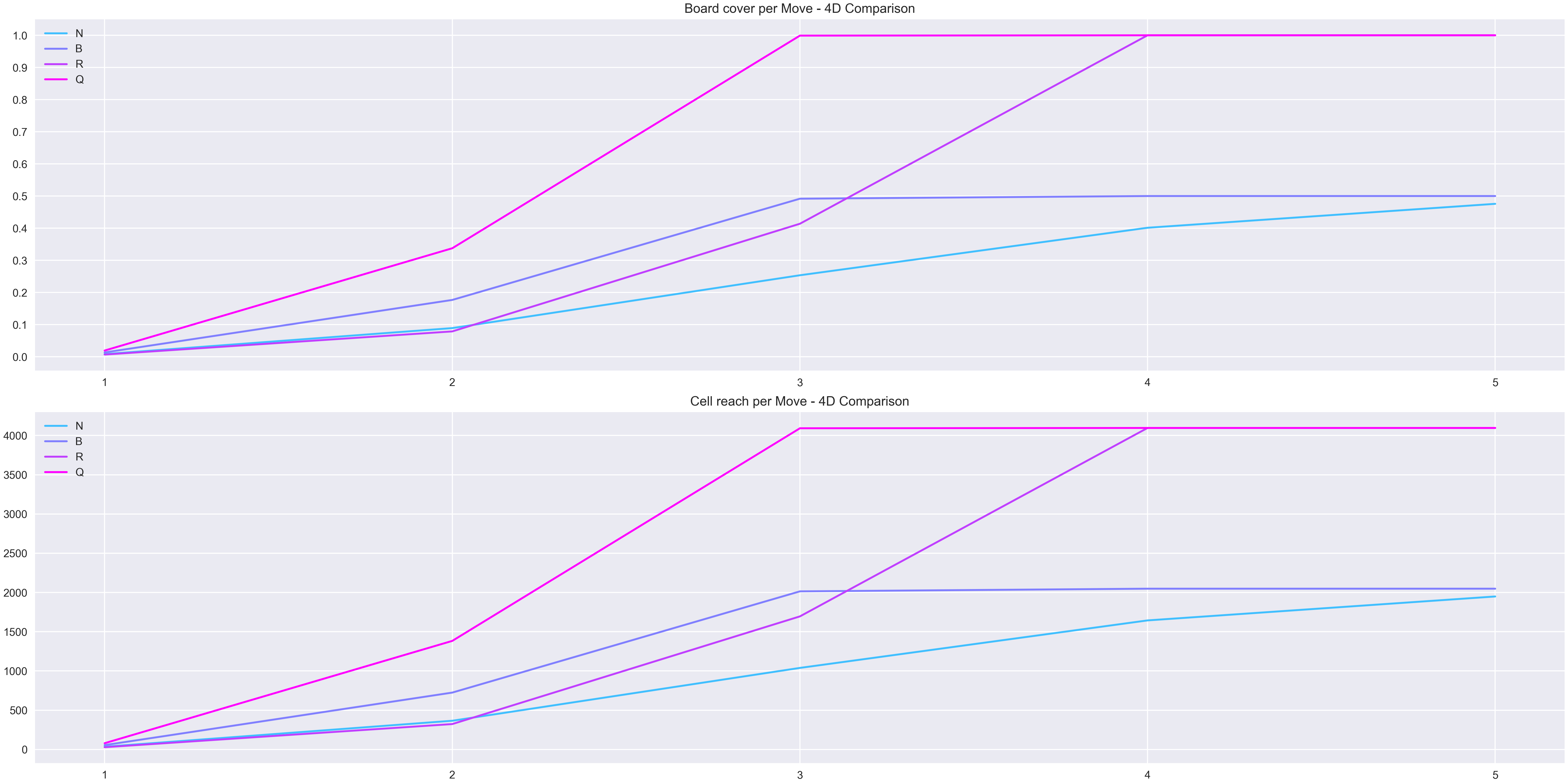
The 4th dimension the pattern that was arising in the last dimension repeats and grows. The rook piece loses even more advantage compared to the rest of the pieces. On this occasion the bishop surpasses the rook up to the first 3 turns/moves, before the rook regains its advantage, but in addition to this the knight it’s also able to gain a tiny advantage over the rook up to the 2nd turn. The graph also shows that in the case of the first turn/move the difference of reach between all the pieces has become negligible, and all of them round the 1%.
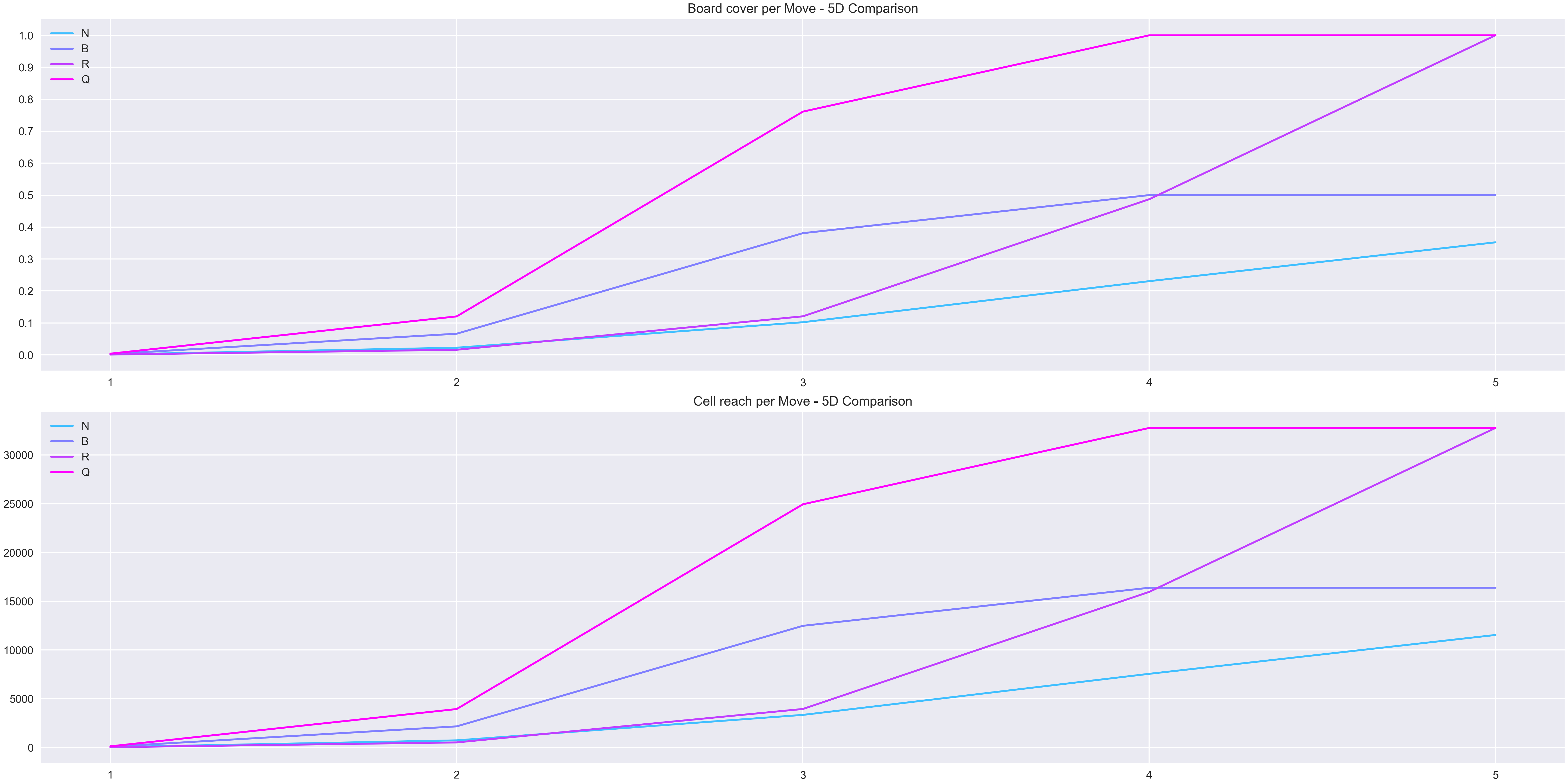
Finally, the last dimension tested (5D) confirms the pattern seen in the previous 2 dimensions, for the rook piece higher dimensions means losing advantage on the initial moves compared to pieces like the bishop and knight. This time the bishop manages to reach more cells up to the 4th move. Additionally, the difference between the initial reach of the pieces once again is negligible.
In conclusion, the analysis of the chess pieces movements in the 2nd, 3rd, 4th and 5th dimensions illustrates the evolution of the piece’s flexibility, reach, and freedom of movement that each one possesses. Then the comparison of the different pieces, shows how the usual hierarchy of the pieces (from most important to least: knight, bishop, rook, queen) it is maintained (at least in terms of movement) the more moves a piece takes, however it also shows that the rook is a piece that suffers the most in the first movements on higher dimensions at points reaching less cells than pieces like the knight and the bishop.


