
Fractal growth refers to the development or expansion of structures or patterns in a way that exhibits self-similarity at various scales.
Fractals are often characterized by intricate and complex shapes that can be created through iterative processes for efficiency and structurability.
Fractal patterns assist us with research into climate change, trajectory of meteoroids, cancer research by studying mutation of cell growth, physics, geography, etc.
Exploring the Helge Von Koch Snowflake, which starts with an equilateral triangle, with each side then subdivided into 3 equal segments. Followed by outside facing equilateral triangle which is then repeated multiple times.

Mathematics of the Pattern
Number of Sides: Each side of the triangle of 3 sides become 4 sides.
The formula: n = 3 * 4a (a = iteration)
Ex. a = 0,1,2,3…sides = 3,12,48…
Length of a Side: The length of each side is ? of the length of the previous stage. Begin with equilateral triangle with length x, then length is
Length = X * 3-a
Ex. 0-3 iterations, length = a, a/3, a/9, a/27
Perimeter: Since all sides in every iteration is the same, perimeter is number of slides x length of a side. Perimeter increases by 4/3 every iteration.
p = n*length, p = (3*4a)(X*3-a), p = (3a)(4/3)a
Ex. 0 – 3, perimeter is 3a, 4a, 16 a/3, 64 a/9
ITERATIONS
VARIATIONS IN FORM

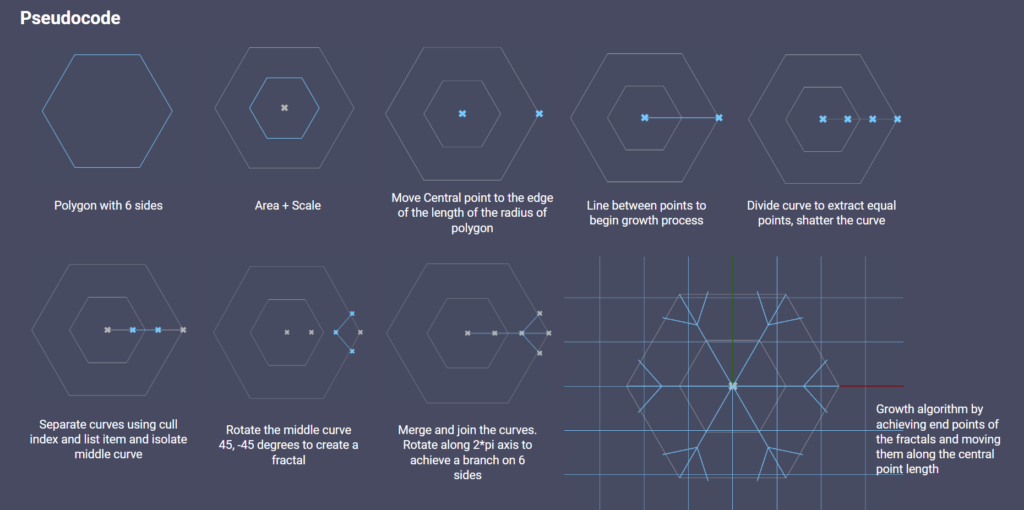
FORMING THE SNOWFLAKE – LOGIC
A central point is used to create a polygon with 6 sides and a radius, with points on each edge to create a line from central point to the edge points
Anemone loops begins with humidity parameters as attractor points within a rectangle.
The increase in humidity would allow the snowflake fractals to grow, equally on 6 sides, with a factor of 10
The aim was to reduce the length of the branches as the snowflake grows, which was done using series with a step value.
The direction of the growth was set based on the original lines and edge points on the hexagon, from where the branching out fractal lines were formed
The branches were rotated 45 degrees on either side of the main branch to create a fractal, which is them replicated based on the number of iteration.
These set of lines are the input into anemone’s loop end command
Once the anemone loop was achieved, the output result was taken to create a 3D snowflake with thickness and rounded edge for a crystallized appearance
FORMING OF THE SNOWFLAKE
GROWTH DATA
VARIATION

