The Advanced Digital Tools course on the MAEBB program focuses on emergent parametric design rooted in algorithmic design principles.
Throughout history, architects and designers have deployed tools and technologies to create, represent and communicate ideas relating to design of physical 3D space. As new technologies emerge – perspective, drawing utensils, for-finding techniques, the invention of modern computers – so the architect’s tools evolve to progress innovation and design. After several decades of computer-driven technical development and digital design advancements, contemporary architecture is now heavily influenced by such multi-parametric form-finding.
It was in 1939 when the term “Parametric Architecture” was first coined. Luigi Moretti, an Italian Architect, defined the term during his research into the “relations between the dimensions dependent upon various parameters” and used these methodologies to propose sport stadiums shaped algorithmically by calculating isocurves that attempted to optimize views for every position in the stadium whilst optimising concrete costs. 1
Fig 1. A model of stadium N by Luigi Moretti. The stadium derives from a parametric model consisting of nineteen parameters2
Indeed, in Barcelona itself, Antonio Gaudi demonstrated one of the earliest instances of parametric design in his use of weights and string to create complex vaulted ceiling geometries in the Church of Colònia Güell. These methods, whilst analog in nature, incorporated the main features of a computational parametric model: input parameters (weight, length of string, anchor point location), equation (gravity) and output (locations of arc vertex) and used these outcomes to inform the resulting structure. Instead of manually calculating the results of these equations, they could be derived from his model and the force of gravity acting on the strings. 3

It is these early examples, pioneered by those like Gaudi, Otto and Moretti, that underlie the methodologies taught in contemporary, digital architecture and which set the precedent for our exploration into parametric design through computational tools. On the Advanced Digital Tools course at IAAC, students are taught the fundamentals of node-based programming, the strategies to build algorithms, the basic concepts of generative design, how to apply data into design logics and how to create dynamic modeling based on defined parameters. Today, parametric modeling is present on most contemporary architecture projects and what follows is a journal of my learning as I familiarized myself with the concepts and tools.
Exploring grasshopper scripts
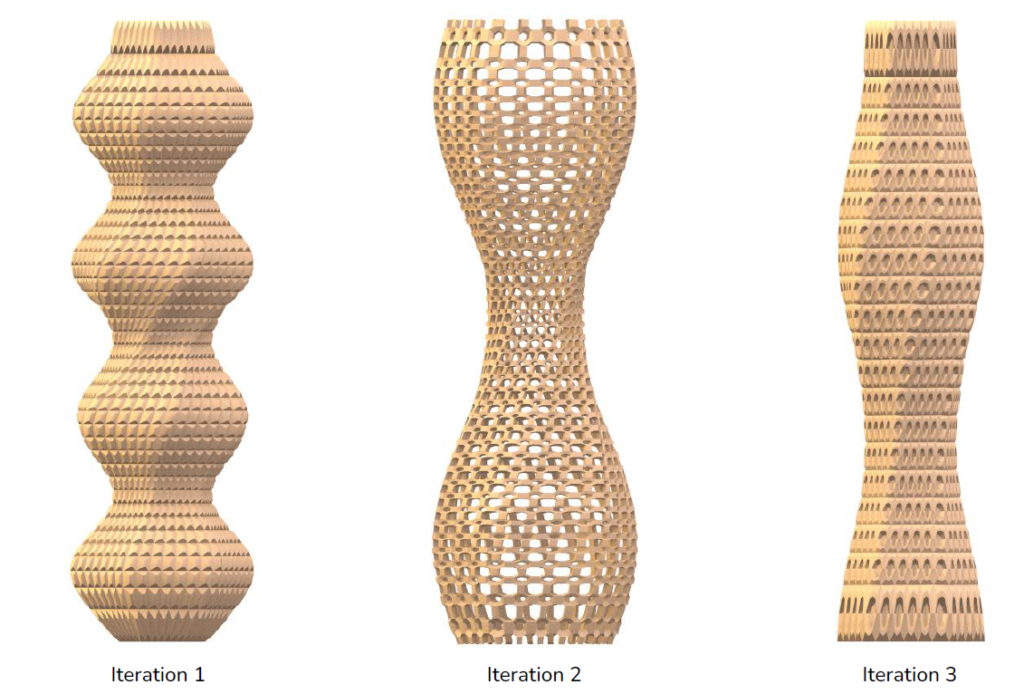
This exercise sought to generate parametric geometry of a basic revolve function, where both the revolution profile and axis were controlled parametrically. Variables were written into my script to drive iteration in design; the axis point A and B locations, as well as multiple points that drove an interpolated curve through their orientation in X,Y,Z.
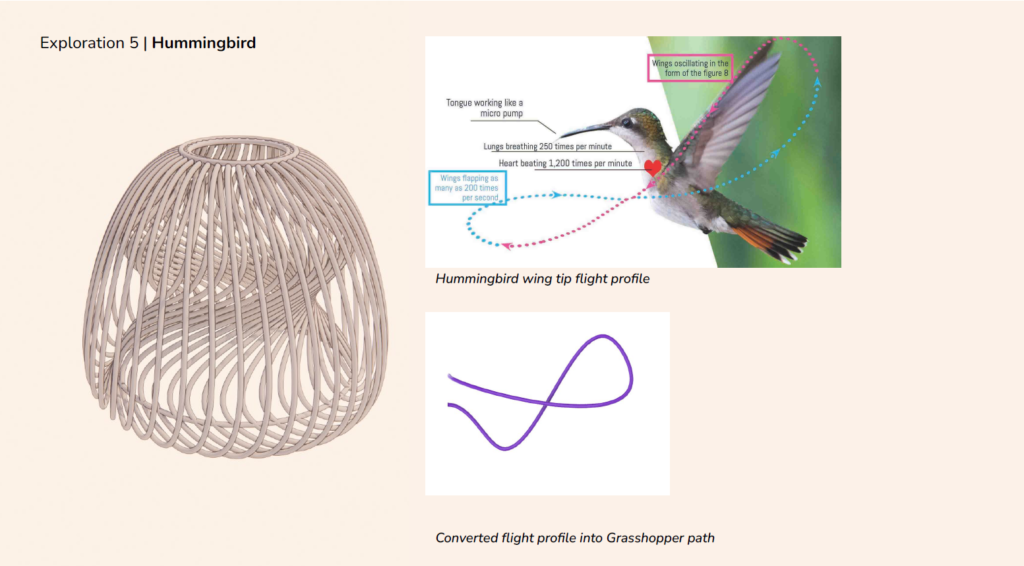
For this exercise, I looked at the wing-tip profiles of various bird species to inform the shape of my revolution profile and the resulting geometry. Through these iterations, I learnt the basics of script-based modeling whilst exploring the opportunities to iterate and adjust geometry by controlling defined variables.
Lists, data matching and data management
Data management is a fundamental component of parametric modeling and was the focus of our next exercise. In Grasshopper, data is manipulated instead of digital 3D objects. A Grasshopper script, or algorithm, is made up of a network of data streams that drive geometry. To manipulate that geometry, it is necessary to filter, divert and modify data.
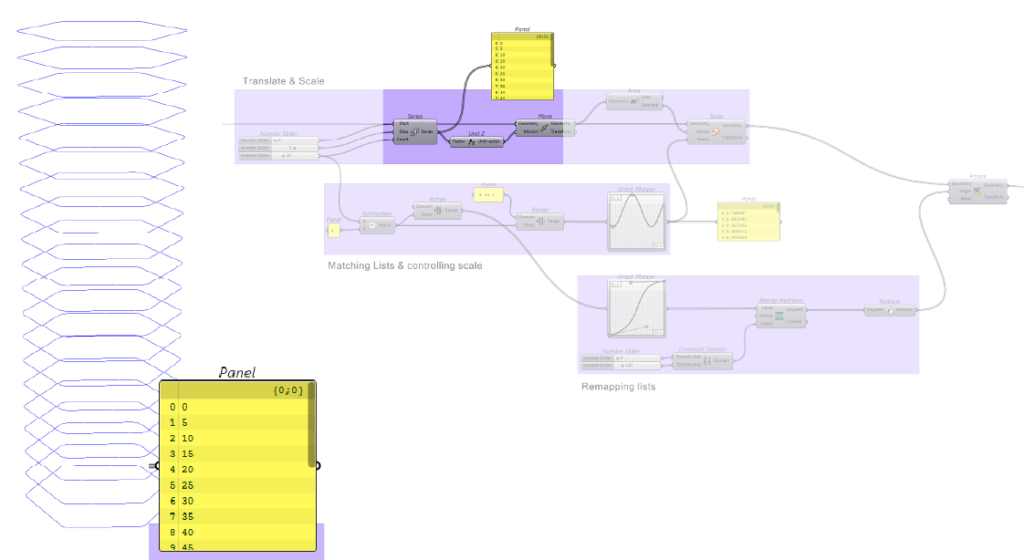
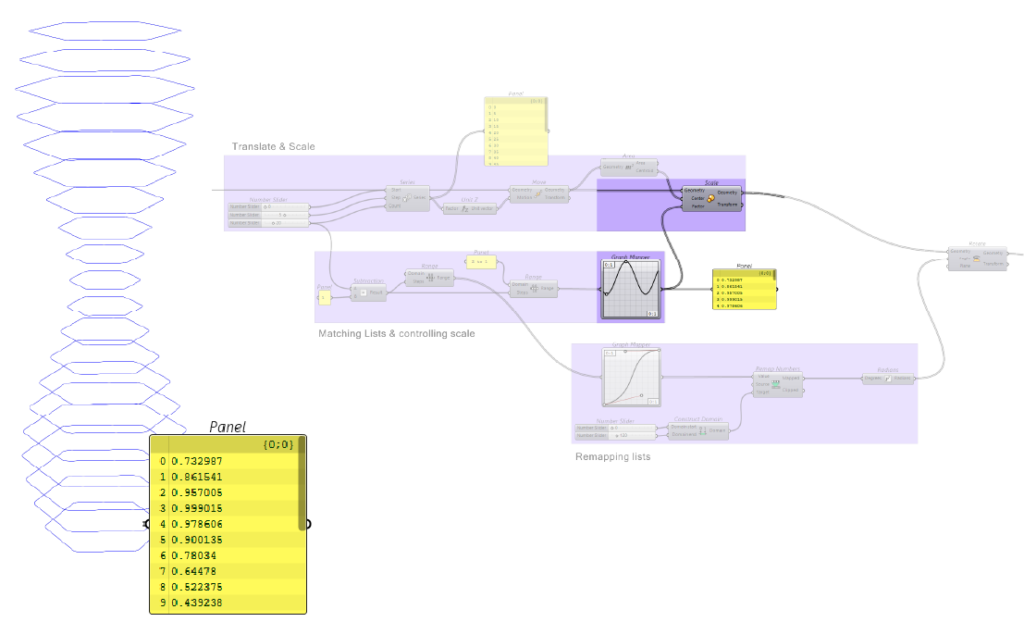
In this exercise, lists of data were manipulated and matched to control the geometry of a twisting tower. A tower was constructed from a series of polygons before being scaled and rotated parametrically. To control these parameters, the list which generated our polygons were matched with a new list of values in a range from 0 to 1. This range was controlled by a graph mapper before being fed into a scale command with a variable scale factor. Matching lists in this way and controlling data allows high degrees of control when manipulating geometry.
Attractors and conditional statements

Attractors are points or curves that exert an influence on the geometry of a Grasshopper definition. They can be used to create complex and dynamic forms that respond to specific conditions. Similarly, conditional statements can control Grasshopper definitions based on certain conditions – creating relationships between different parts of a definition.
Using these two methodologies, the following facade was created from an alternating brick pattern (controlled by a conditional statement) and a subsequent rotation of brick elements controlled by an attractor definition across a control curve.
Manipulating lists to control geometry
As we learnt earlier in the course, lists are a fundamental part of Grasshopper and are used to store and manipulate data. Lists can be created manually or specific components can be used to generate them. Lists, once created, can be manipulated by a variety of components which gives targeted control over the data.
In the following pavilion example, the wave pattern was generated from two series of control points (blue points) where alternate points were selected using a cull pattern function which were ultimately used to drive a wave-like curve (pink curve).
This underlying geometry was used to construct the structure and veneer of this example pavilion and provided key lessons in understanding and manipulating lists to generate and control geometry.
Creating mesh geometry and affecting them with data input
Mesh geometry in Rhino and Grasshopper is a 3D modeling approach where geometry is described by faces – represented as triangular, quadratic or n-gon and are organised to describe the boundary of an object. Meshes make large, complex geometry easier to compute and are useful when creating dynamic geometries.
Mesh geometry can be manipulated by data. To explore this, I used the Ladybug plugin to analyze sunlight data over an Eixample apartment block in Barcelona, Spain. The resulting data from this analysis was used to affect mesh geometry on the rooftops; more sunlight = taller structures.
Using the Weaverbird plugin, the affected mesh can be controlled in various ways by components such as a Catmul-clark subdivision to smooth the mesh. The script could be very useful to help locate, shape and design greenhouse structures which were responsive to their environment.
Animating geometry
Animation is a useful tool in Grasshopper to help display and communicate a number of design decisions, design process or iterations through parametric code. For this example, animation was used to step a viewer through the construction of a parametric mesh tower.
Through the examples explored on this course, supplemented by my own research into parametric modeling, I have grown familiar with some of the key concepts of parametric, generative and algorithmic 3D design. The skills and tools learnt have opened up new design possibilities as I move from static computational design into a world of agile, responsive and dynamic 3D design.
- Algorithms Aided Design, Tedeschi, A. 2014. ↩︎
- https://parametrichouse.com/parametric-architecture1/ ↩︎
- https://www.danieldavis.com/a-history-of-parametric/ ↩︎

