Mazes have fascinated humans for centuries. Solving them requires decision making based on limited knowledge, and the ability to remember and avoid previous mistakes. The problem of solving a maze from any given position within it, without knowing the location of the exit lends itself well to the iterative logic that is central to this computational urban design course.
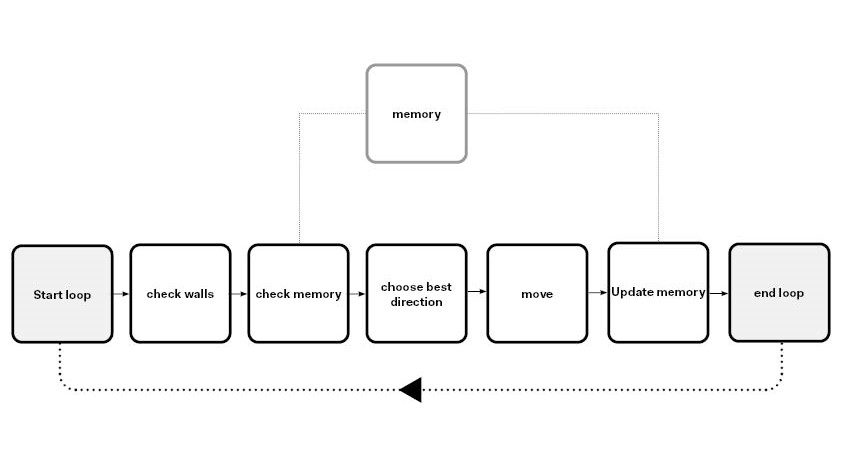
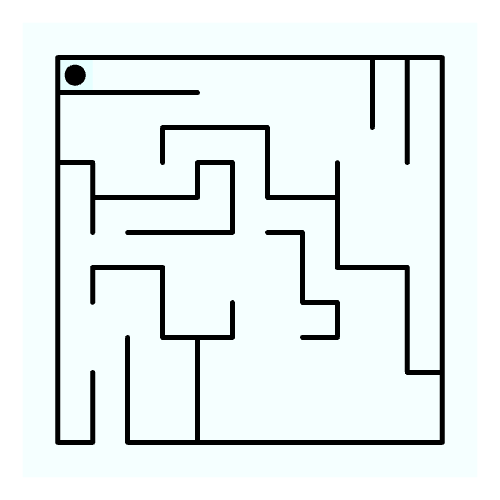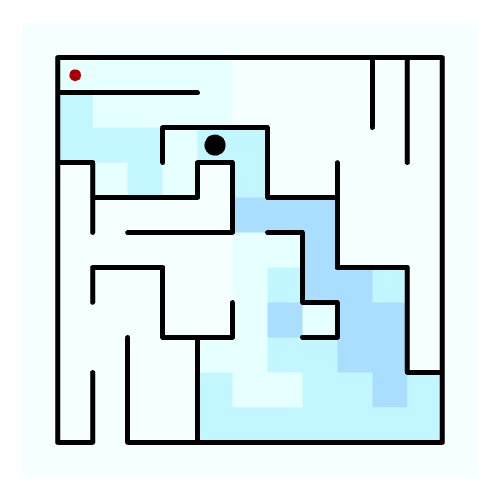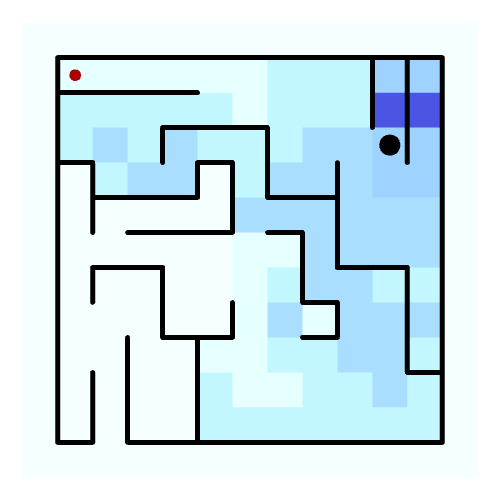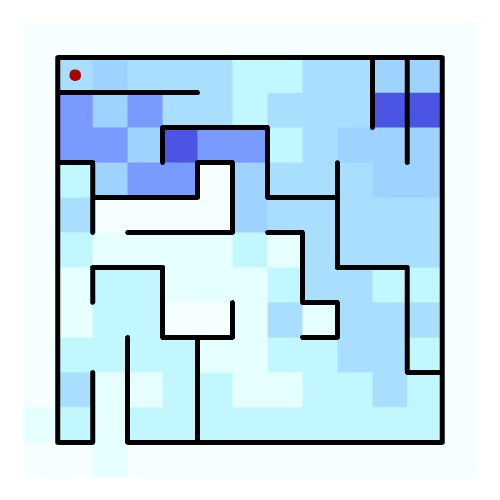
The grasshopper definition used to solve this conundrum assumes a situation where the solver can be placed in any cell of the grid and doesn’t know where the exit of the maze is. For every step the solver checks three criteria: firstly it avoids collisions with walls, secondly it checks its memory (blue) to prioritize unexplored cells and lastly it chooses the direction with the longest uninterrupted space for movement. The algorithm uses a discrete mathematical logic. This means that the maze is understood as a grid where every position has row and column number. The advantage of this is that it allows the system to store the number of times that the solver has visited any given position.
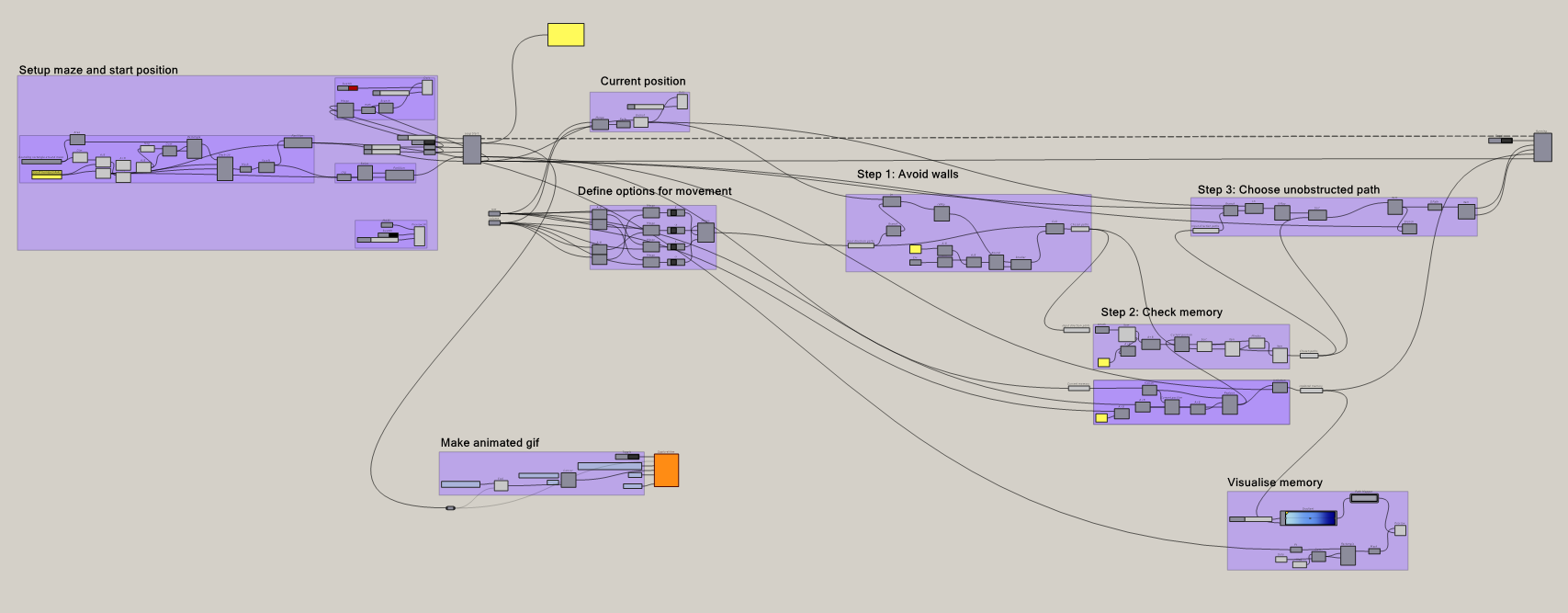
The algorithm is able to solve a variety of different mazes: