Assemblage is a design strategy that depend sin its methodology on computational thinking and following an iterative logic of design to achieve a growth of an accumulative design process. The design is based on designing different building blocks that follows a voxel shaped boxes that grow based on a computational design logic of different iterations that control the growth limits and conditions. The resulted data is then provided in a way that can be used for the robotic arm in a pick and place process with specific connection surfaces of the design component.
Computational growth
A component of four voxel boxes were developed with providing it with three planar surfaces as connection joints in the assembly. A collision check of nine possible permutations was tested and excluding the colliding permutations to avoid them resulting in 7 successful and 2 unsuccessful permutations as shown below.
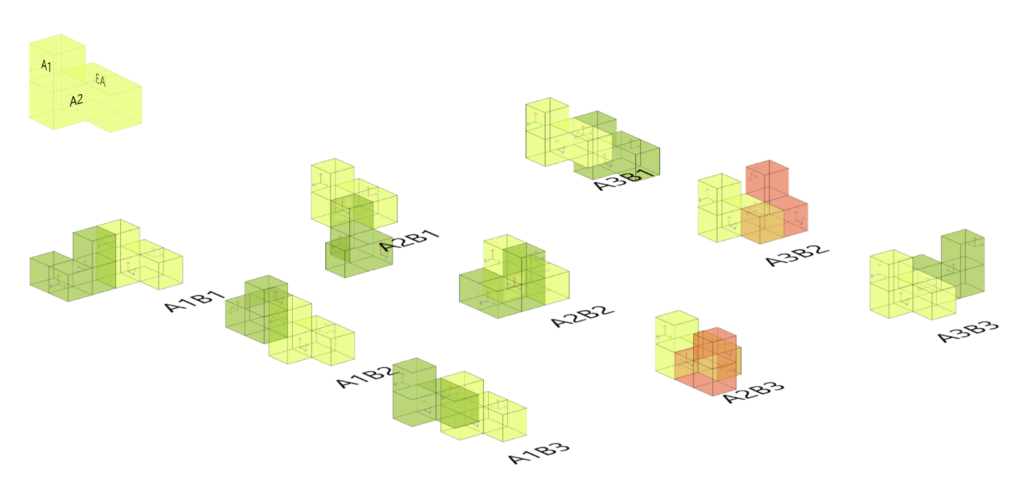
By changing the connection planes and its rotation, a various assemblage options were generated with random seed of 100 iterations for each assemblage. The results reflect different results that can show compactness, spreading and complexity of the resulting assemblage as shown in the figure below.

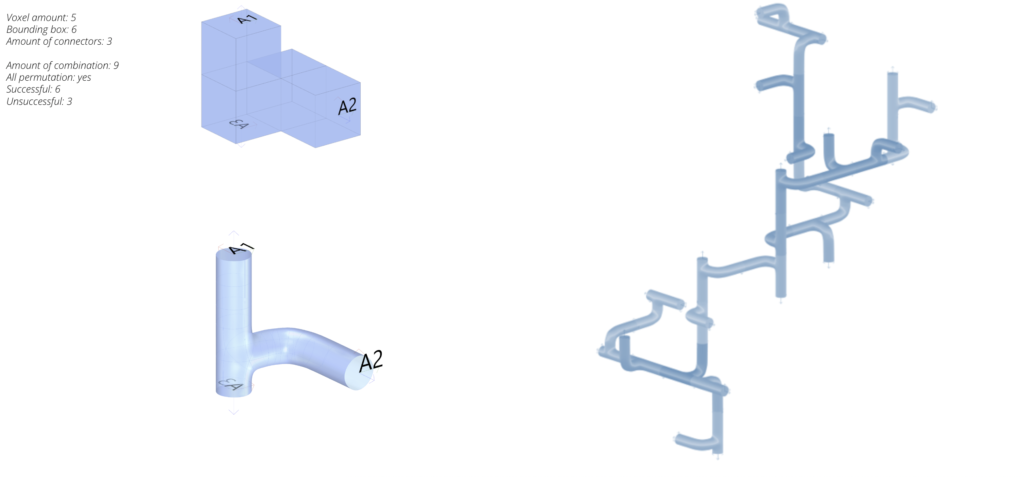
The same process was then applied to different components with different building block shapes in order to explore the assembly concept in various results. In this component the connection planes were provided in a way that resulted into 9 successful permutations without any collisions.

By following the same methodology, new interesting iterations were generated that can follow some specific logics like growing in a linear form or a cubic form as noticed in the diagram below.

A trial of replacing the boxes volume with a pipe like design was provided as a way of exploring the several design options that can be generated based on the voxel design blocks as shown.
ASSEMBLY LOGIC
After exploring the possible iterations and random designs that can come of very simple changes, a specific logic map was designed to guide the generated iterations basing it into a loop system. the logic followed a sequence of generating the connection joints, checking for possible collisions for the new generated permutation, then providing a filtering methodology for the growth of the design for 100 iterations, then finally removing any occlusions and repeat …

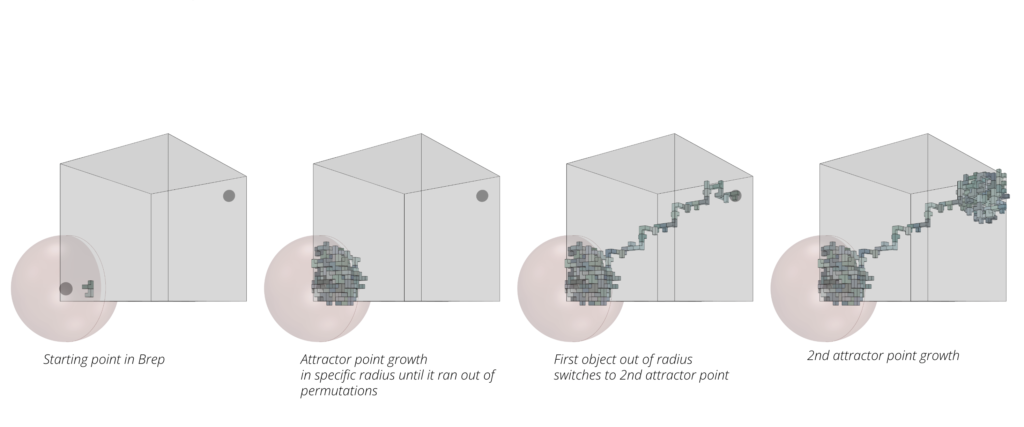
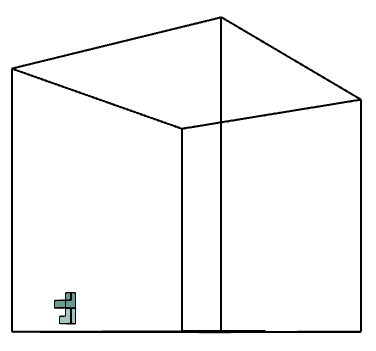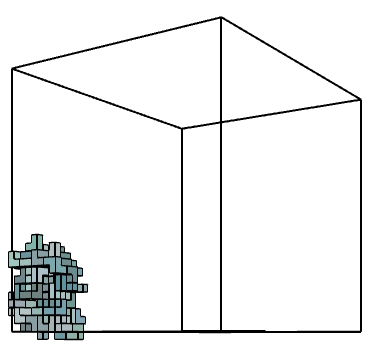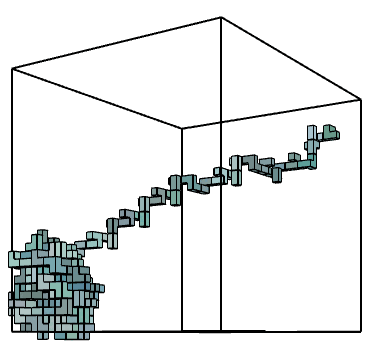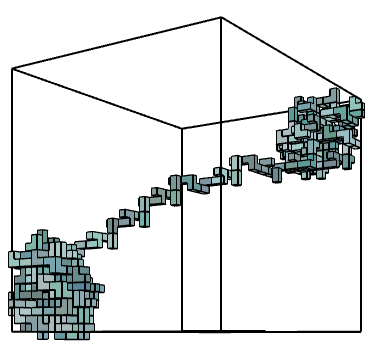
The growth logic developed was based on having two attractor points with a specific distance that when the growth get all the possible iterations within this distance, it switches to the other attractor point using the easiest way to reach, and then start growing around it. All of this should happen under the provided condition of growing inside a specific geometry -which in this case provided as a cube in the illustration below.
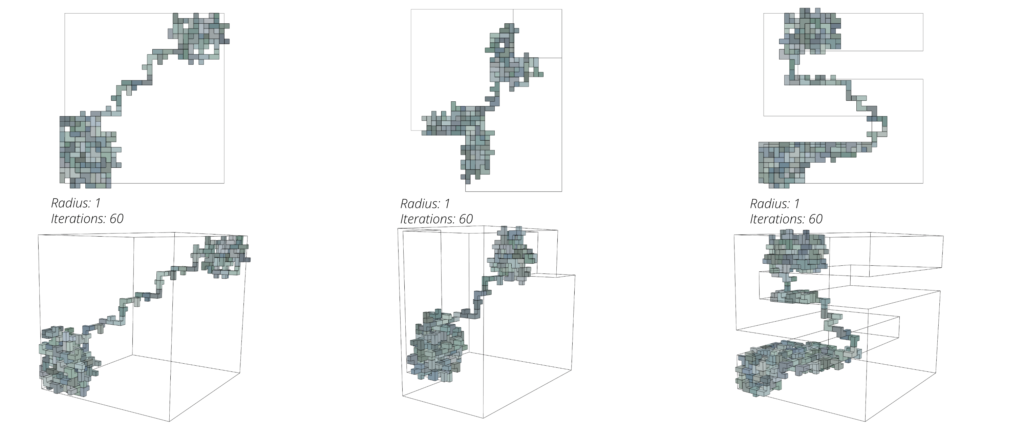
By using different connection planes and different angle of rotation, three trials were made of 200 iterations in order to observe the different behavior of the growth to reach from one attractor point to the other with keeping the Brep geometry, switching distance and the number of iterations constant. Some observations were made based on the results, for example if a fastest connection would be needed then option 3 in the pictures below would be the best fit; or if a perpendicular connection is needed then option 2 would be a better fit because its connection planes are in opposite directions of 180 degrees.



The logic was then applied to the different originated components with different joint connections to explore the various results that are generated from the logic and to have more analytical approach towards the useful applications of the different iterative results for every component on its own.

The growth logic developed was based on having two attractor points with a specific distance that when the growth get all the possible iterations within this distance, it switches to the other attractor point using the easiest way to reach, and then start growing around it. All of this should happen under the provided condition of growing inside a specific geometry -which in this case provided as a cube in the illustration below-.


apPlications exploration
The computational iteration concept was then used a further step in the bigger design scale as a trial of exploring and applying the concept on bigger scale buildings by providing a small flat element that resembles the component used with providing some solid sides as connection joints that can iterate a bridging type of connection between buildings or many other uses.


Another application was explored by designing an elevation item with timber bars to form a mass of interlocking bars that grows over two attractor points on the building geometry with a maximum expansion offset from the building.



