XX WS3.1 XX
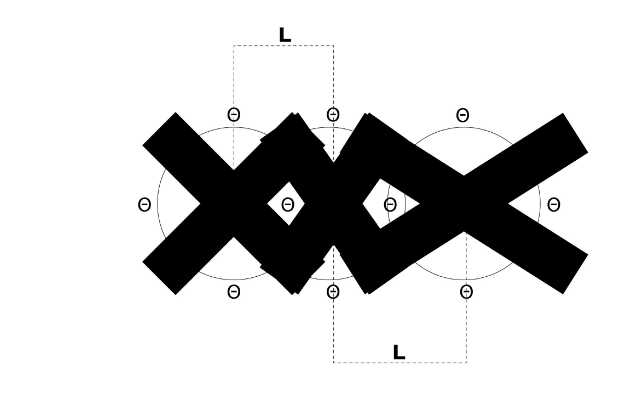
How can we compress the soul of a 3D object into a few pixels?
Kapla Kadabra explores the magic of encoding geometry into 2D data structures – and bringing it back to life.
XXXXXXXXXXXX AIM XXXXXXXXXXXX
This project explores a lightweight method to encode and decode 3D geometries into pixel matrices. Instead of storing geometry through conventional mesh or point cloud formats, we translate spatial data into 2D image structures, where each pixel contains information about point positions and rotation angles.
This system has several potential applications, from compressing geometry data to enabling neural networks to learn and generate spatial configurations directly from image-based inputs.


XXXXXXXXXXXX ENCODING THE FORM XXXXXXXXXXXX
Our system encodes the X, Y, and Z coordinates of a 3D model into pixel values, assigning each axis to specific channels in a 16×16 or 32×32 image matrix. For example:
- X and Y coordinates are mapped into two color channels (R & G),
- Z coordinate and Θ (rotation angle) are encoded using the B channel or separate grayscale images.
XXXXXXXXXXXX DECODING THE GEOMETRY XXXXXXXXXXXX
The decoding process reads the image matrices and translates pixel values back into numerical spatial coordinates and rotation angles. Using consistent normalization and value ranges, we are able to recover a geometry that closely matches the original input, with minor deviations due to pixel rounding and color quantization.
This decoding was validated in both trials and serves as the base for integration into learning pipelines.
XXXXXXXXXXXX TRIALS & ITERATIONS XXXXXXXXXXXX
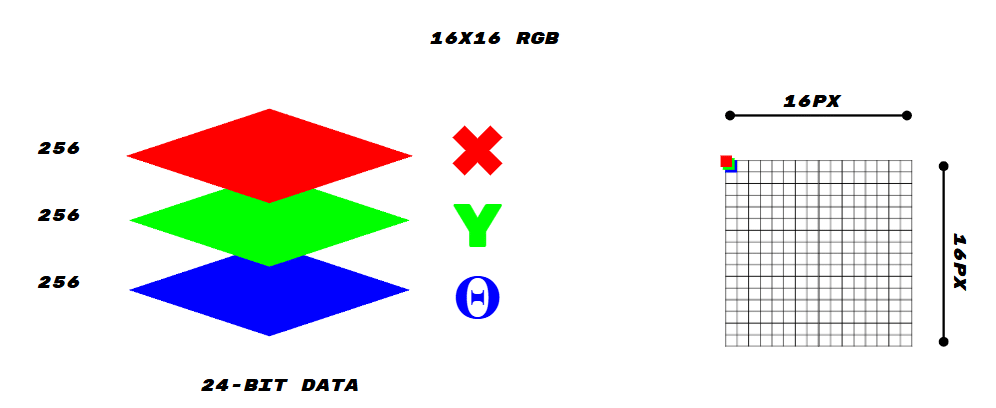
Trial 1:
- Image size: 16×16 pixels
- Channels:
- Red → X
- Green → Y
- Blue → Z
- Rotation angle stored separately
- This version stores up to 256 points with 24-bit data. While compact, the precision is limited.

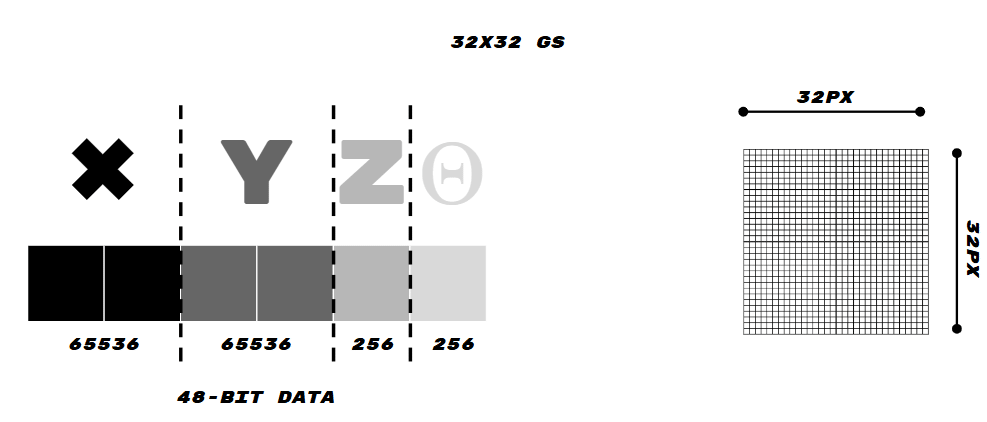
Trial 2:
- Image size: 32×32 pixels
- Each property (Y, Z, θ) is encoded in a separate grayscale channel.
- Data capacity: 1024 points with 16-bit per property
- This allowed greater resolution and independent processing of different features.
- Each pixel becomes a container of spatial data, which can then be used either to reconstruct the original geometry or to feed a generative model.
Both trials were decoded back to 3D models with high fidelity. We used these matrices not only to regenerate the geometry but also to feed them into a GAN (Generative Adversarial Network) to explore the generation of novel forms based on encoded datasets.
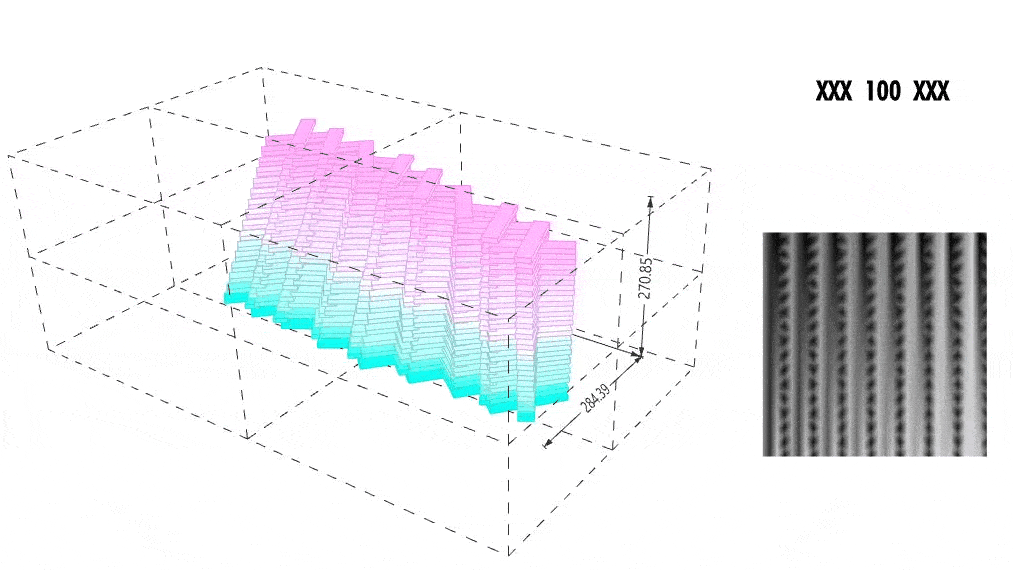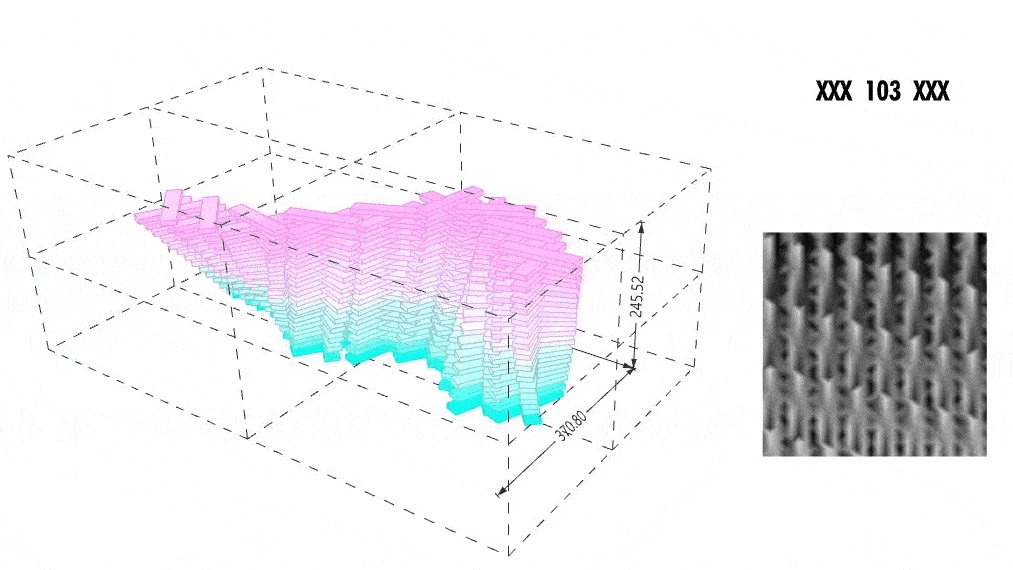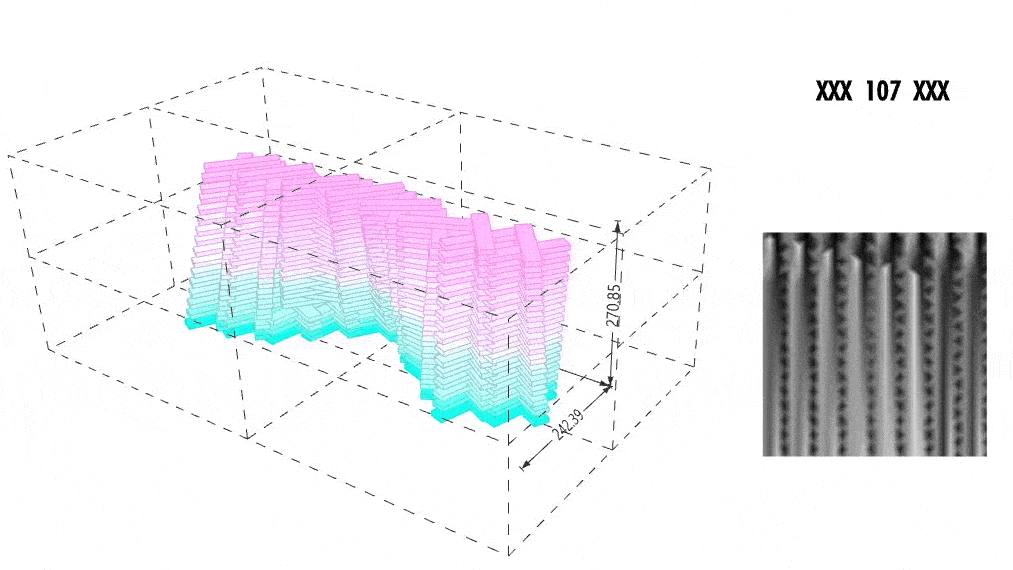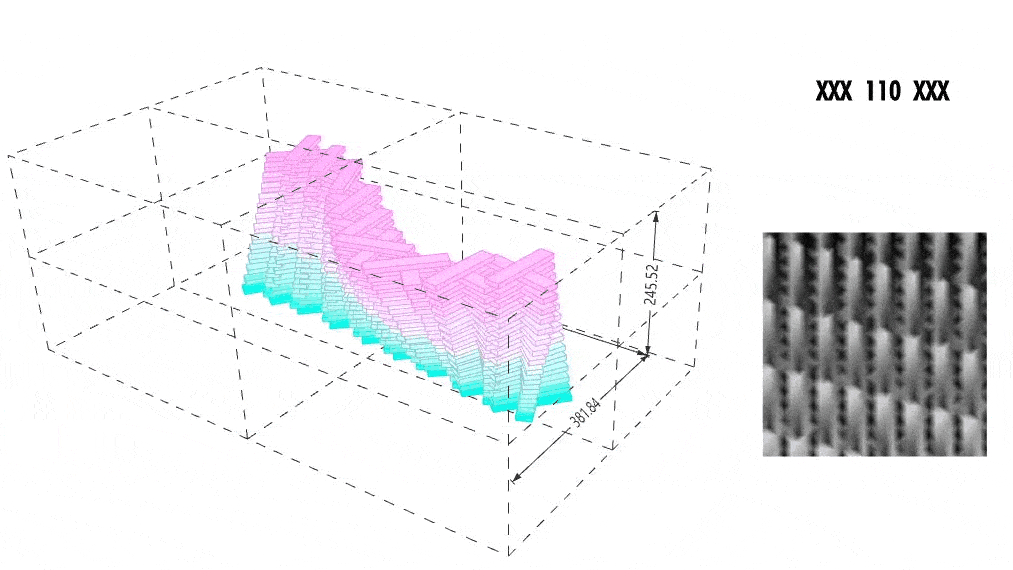
XXXXXXXXXXXX DATA VARIATION & CONTROL XXXXXXXXXXXX
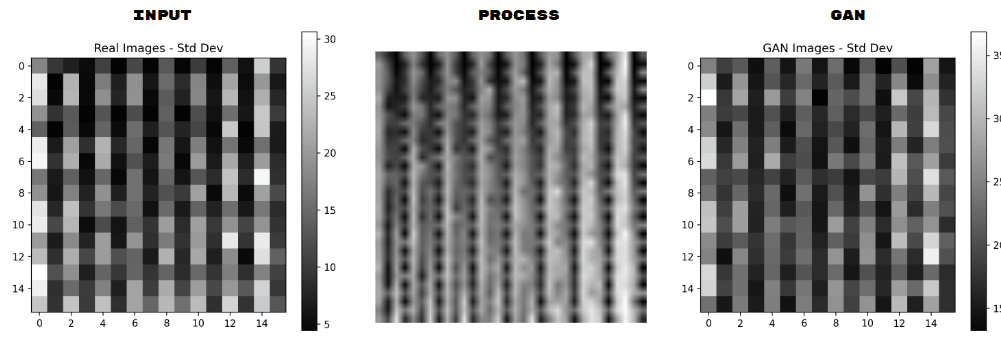
We visualized pixel-level standard deviation to understand which regions in the form were most dynamic. Brighter pixels represented more variation, informing both our GAN training and design tweaking.
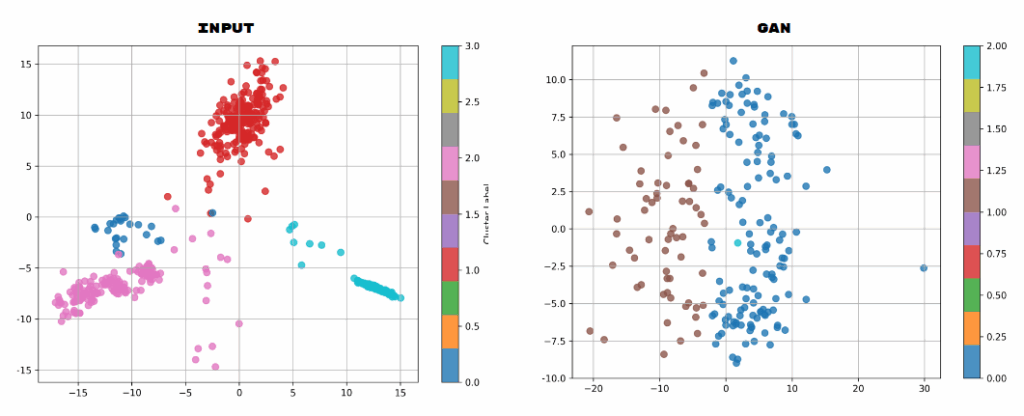
XXXXXXXXXXXX GAN MEETS GEOMETRY XXXXXXXXXXXX
We introduced a GAN (Generative Adversarial Network) to explore how image-based encodings can be used to generate new spatial configurations. Instead of generating 3D points directly, the GAN is trained to output pixel matrices in the same format as our encodings, which can then be decoded into 3D geometries.
This allows:
- Synthetic generation of geometry-like forms
- Easy visual debugging of model output
- Consistent pipeline from generation to fabrication


XXXXXXXXXXXX OUTPUTS XXXXXXXXXXXX
- Encoding/Decoding pipelines
- A collection of encoded forms
- GAN-generated geometries
- Fabricable models derived from pixel matrices

XXXXXXXXXXXX FINAL THOUGHTS XXXXXXXXXXXX
- Precision is affected by image format (8-bit vs 16-bit)
- Rotation angle encoding could be more robust
- Decoding requires consistent normalizations for all datasets
- Encoding resolution is limited to 1024 points max in our current trials
🔧 Future work
- Validate fabrication consistency, ensuring decoded models can be exported for CNC/3D printing with no geometry loss
- Refine encoding strategy to improve spatial accuracy and compression (e.g., using 16-bit TIFF or floating-point formats)
- Develop an encoding tailored for neural network ingestion, with structured layouts, padding, and augmentation in mind
- Train on larger datasets to allow the GAN to learn more diverse spatial logics
- Introduce metadata channels, such as material or type, encoded as pixel overlays
This system opens the door to lightweight, visual-first geometry workflows. Potential use cases include:
- Compact 3D geometry sharing
- Dataset creation for learning-based design tools
- Real-time manipulation of form through image processing
- Embedding geometry into visual media (e.g., QR-style structures)
The long-term goal is to integrate this encoding-decoding approach into a fabrication-aware design system, where geometry can be stored, evolved, and regenerated through visual interfaces and learning agents.
Team
Sasha, Nacho & Neil
MRAC 2025 – IAAC

