
The Concept
The pavilion’s striking, organic form isn’t just aesthetic; it is rooted in the Clebsch diagonal cubic, a cubic algebraic surface defined by the equation:
subject to the constraint:

Mathematical Foundation: The Clebsch Diagonal Cubic
This specific geometry was selected for its inherent geometric stability. To adapt this theoretical form for a physical site, we rotated and scaled the geometry to fit an 8m by 8m by 6m height base domain.
From Equation to Lattice

1. Mathematical Definition & Constraint Application
The process begins with the Clebsch Diagonal Cubic, a complex cubic algebraic surface. The geometry is defined by its specific equations that are solved and constrained.
2. Geometry Definition & Discretization
The continuous mathematical surface is converted into a high-resolution mesh. This mesh serves as the geometric boundary for all subsequent structural layers.

Geometry Definition: From Surface to Lattice
3. Lattice Generation
Using the plugin Crystallon, we fill the mesh volume with a structural lattice.
- Twisted Box: The mesh is divided into “twisted box” volumes that follow the curvature of the surface.
- Cell Type: Within these boxes, an Edge Octahedron cell type is applied to create the intricate webbing of the pavilion.
4. Boundary Conditions & Structural Analysis
The model is then imported into Alpaca to simulate real-world physics.
5. Optimization (Galapagos & Millipede)
The final stage is an iterative loop focused on performance.
- Millipede: This tool is used for stiffness optimization, identifying which parts of the lattice need to be thicker to handle stress.
- Galapagos: An evolutionary solver, is used to automatically test hundreds of variations to find the best option that minimizes both mass and deflection.

T0POLOGY OPTMIZATION
By proposing beam radius as .05 m and Material Name: Glass reinforced recycled PET we started optimization for stiffness distribution map on the pavilion mesh to use it as guide for next analysis by alpaca
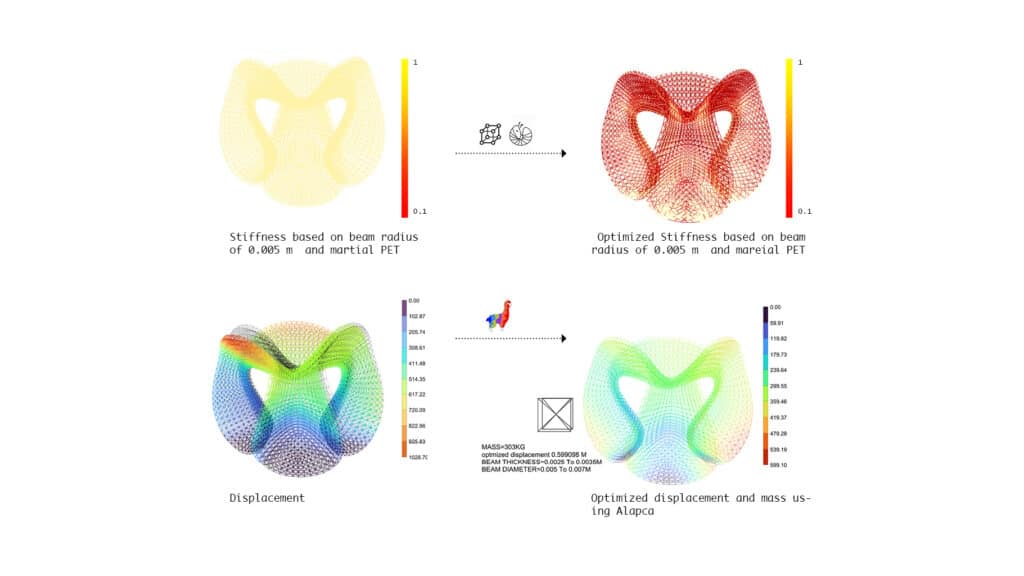
Lattice Optimization
To define optimum solution we used Alpaca +wallacie to run evolutionary optimization inside grasshopper by defining fitness objectives as lowest amount of displacement as well as mass
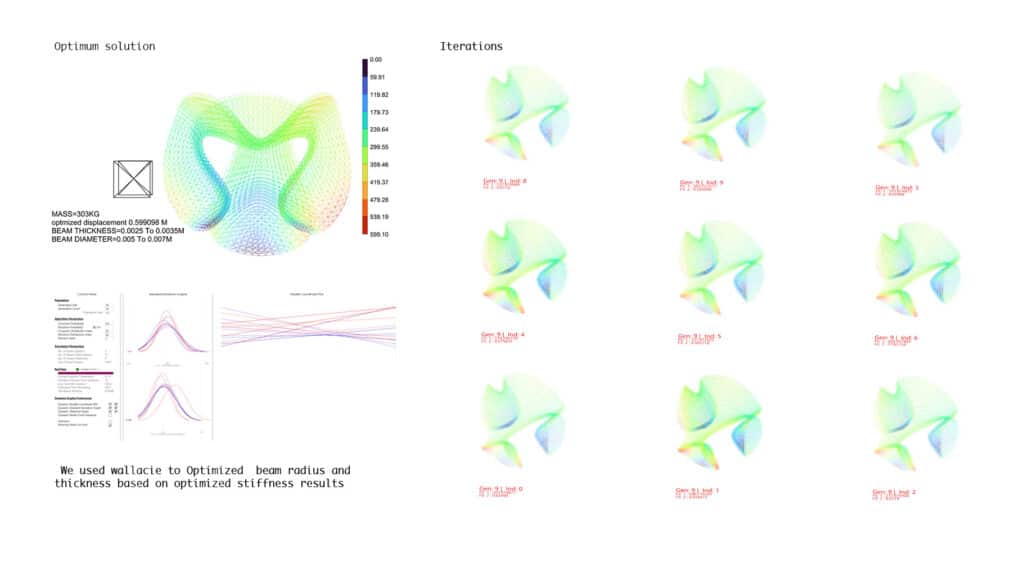
Lattice Modules
by exploring different lattice module shape we managed to define best configuration for lesser mass as well as displacement

A Vision of Sustainable Complexity
The final result is a pavilion that feels both futuristic and deeply grounded in historical mathematics. By using recycled PET reinforced with glass, the Clebsch Pavilion demonstrates how complex, optimized geometries can be realized through sustainable material choices.


