
Nestled within the crater of Agnano in Naples, Italy, this museum lies at the base of a dormant volcano. Spanning multiple floors, the collection unfolds the captivating narrative of the native species of Naples.

Our project germinates from three distinct mathematical equations: A cartesian equation that produces a Clebsch diagonal cubic surface, a parametric equation for generating a spiral, and another parametric equation representing a cylinder.
The Clebsch surfaces’ three central openings function as catchers and amplifiers of the soundscape enveloping our building. Simultaneously, the spiral and cylinder serve as means for visitors to circulate vertically and horizontally.

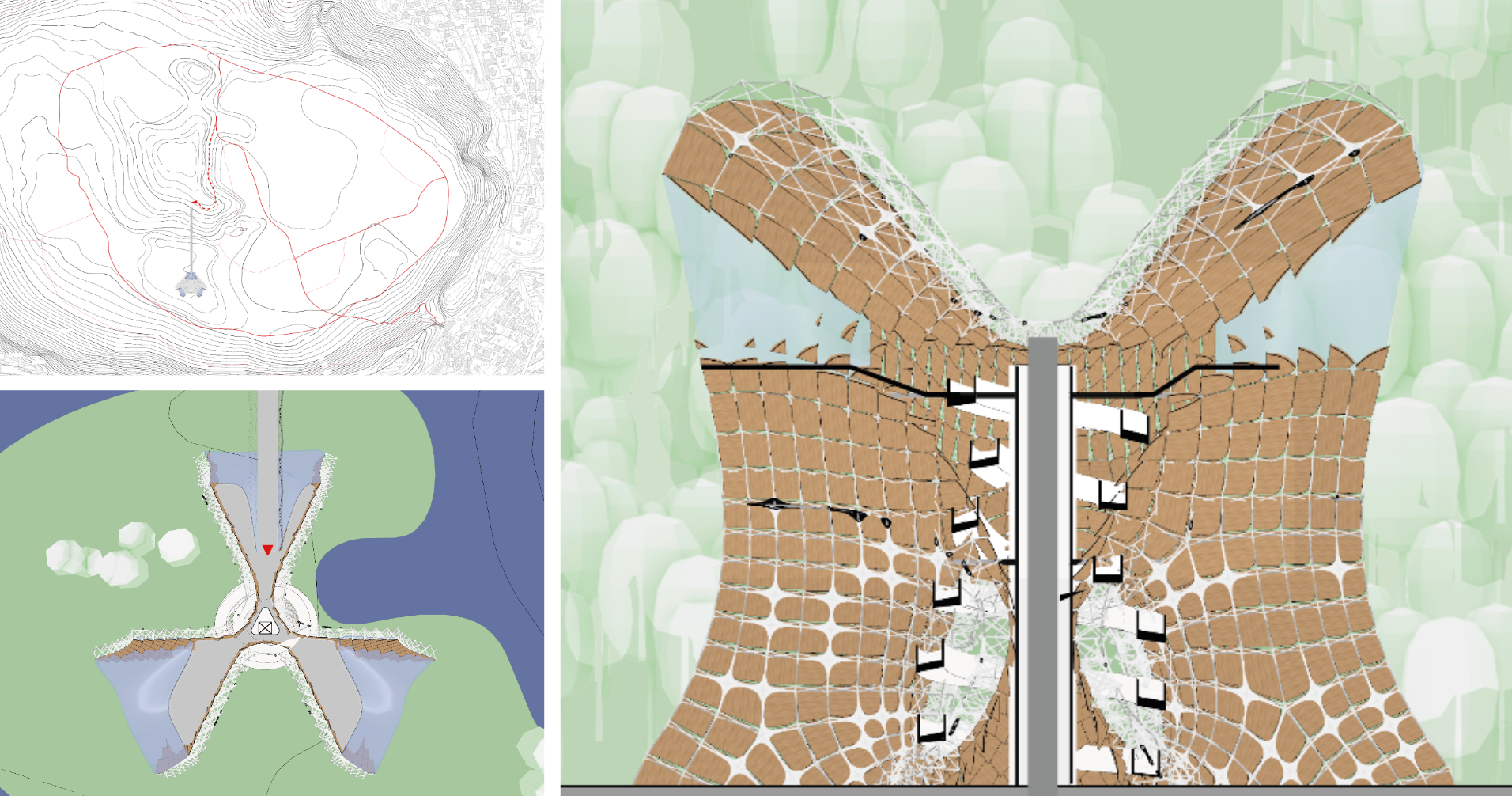
Carefully placed at the lowest topographic level, the building is vertically stretched to maximize the three central openings. This captures as much of the soundscape as possible, creating the space required for exhibition galleries. Three enclosures augment each building opening.
Visitors approach the main building via a bridge and navigate the galleries using the spiral ramp.
The main building’s facade or skin comprises three layers: Interior wooden panels, which would provide the visitors with multiple overlapping reflections to the direct sound from nature; a metal space frame, and what we affectionately term “sparkles” – a series of 4 edges light-emitting components.

Various transformations, such as rotation, movement, and scaling, were applied to the Clebsch surface until the necessary space for the central spiral ramp and gallery floors was achieved.
The space frame originated by offsetting the vertices of the original mesh outward and conducting a topological search, filtering vertices based on the number of adjacent inner edges.
The filtered vertices from the prior step underwent a 50% random reduction. Only vertices with four adjacent edges were selected and converted to pipped subDs.
The bridge utilizes an undulated surface created with sine curves, subsequently amplified and modified.
The bridge cylinder underwent cutting and transformation using sine curves, amplified and extracted from its original surface within a variable range.

The building’s surface was determined by varying its iso-value range from -10 to 12. The resulting surface underwent “squeezing” in the x and y directions, ranging from -5 to 2.
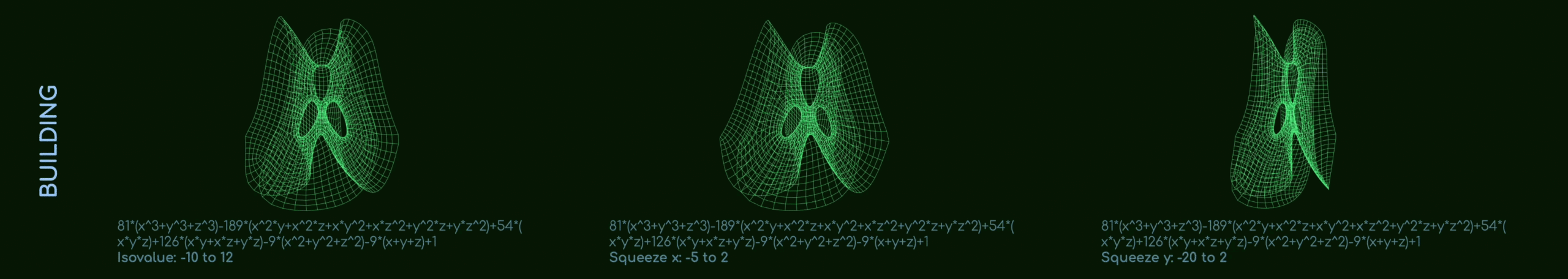
The interior panelling on the building follows three steps: reordering the vertices of the mesh faces and filleting a corner of every face by re-trimming it based on 3D trim data from a base rectangle. This filleted corner was pulled from the main surface to admit natural light into the building.

The museum’s pinnacle transforms into an observation deck. Envisioned with a panoramic vista of the Agnano volcano, complemented by a concave structure housing acoustic installations, this design aspires to offer visitors an unparalleled “Immersive Audiovisual Environment.”

The site plan shows that the museum connects the bridge to the local route. The plan shows the main entrance at a height of 20 meters. The conceptual section shows the idea of the vertical exhibition space.
All our equations were translated to Python using Co-Pilot, allowing us to input them into a GhPython component.
Several attempted spiral equations exhibited non-planar sections and had to be discarded.
We discovered that cartesian and parametric equations necessitate different implementations. The IsoSurface component from the Jellyfish plugin was crucial in obtaining our Clebsch surface.
Finally, the meshing process yields unorganized vertices, resulting in twisted panels. We rectified this issue by adjusting the vertex’s Z value.


