Studies on Fractal Growth – Computational Desing II

The term “fractal” was coined by the mathematician Benoît Mandelbrot in 1975. Mandelbrot based it on the Latin fr?ctus, meaning “broken” or “fractured”, and used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature

In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of the Measure Theory.

Influential factors for the analysis

“A fractal is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole”  Benoit Mandelbrot

Parameters that define fractals:

1. Starting geometry
2. Scale of the division, or, in how many parts the initial curve is divided
3. How the divisions are arranged, in which angle they are positioned 

Parameters that don’t influence on the fractals behaviour:

1. Measurements, or start and ending. A fractal in an infinite multiplication of itself, therefore do not depend on an specific measurement or scale apart for visualization purposes 

Project Goal: understand and demonstrate the generative process that creates the geometric pattern of fractals exploring its variations and limits

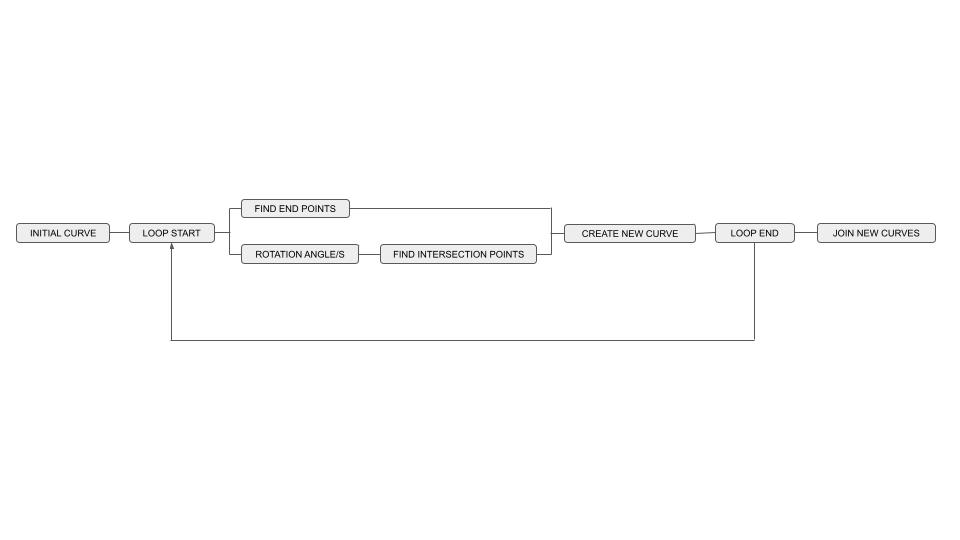
Recreate the Heighway Dragon Pattern in Grasshopper

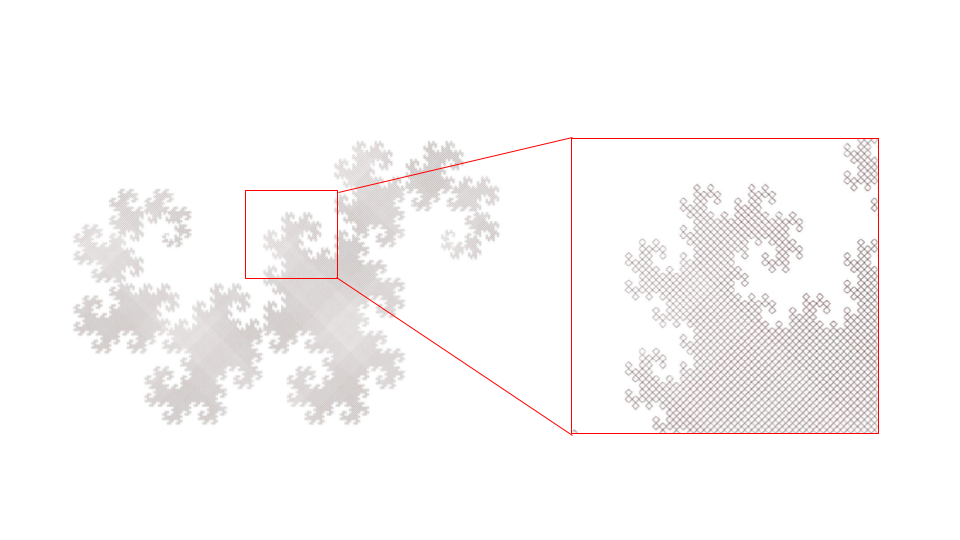
Research Exploration 01 – Linear Fractals 

Goal: To explore different iterations of the fractal pattern in a linear way, starting of by a straight line

Variable Parameters

1. Starting curve 
2. Angle of rotation – single variation
3. Angle of rotation – 3 variations within the same pattern 

Non Variable Parameters:

1. Size of curve
2. Number of divisions within the curve 
3. Number of iterations 

Data Collected:

1. Initial curve length
2. Fractal curve length
3. Length growth fractal / initial ratio 

Linear Iterations Catalogue

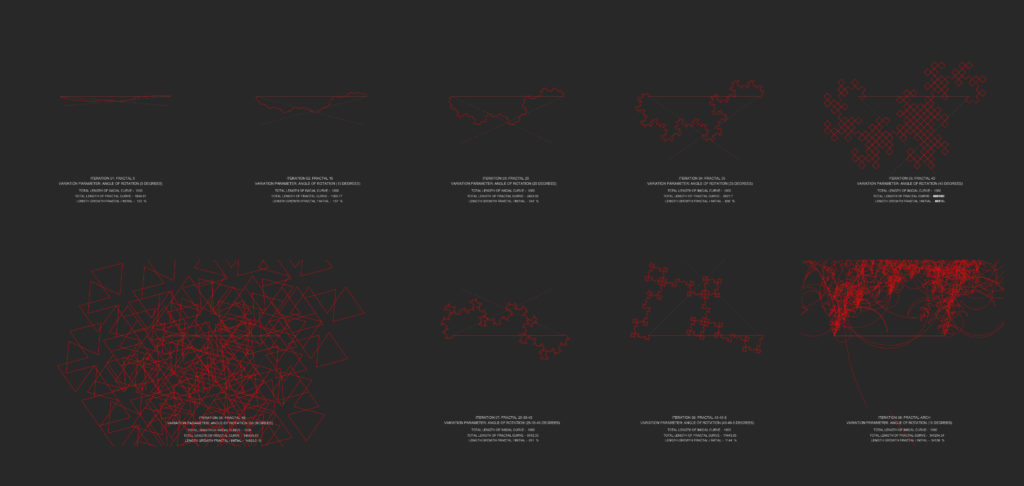
Conclusions on the Linear Fractals Exploration

1. The bigger the angle of rotation as the variable parameter, the bigger perimeter length is, creating a more “ramificated” curve. Meaning, there is an exponential growth proportionally related to the angle of the rotations

2. The bigger the angle of rotation is, less straight the fractal curve will be. For this reason, the curves made out of bigger angles demonstrate more visually the fractal patterns seen in the Heighway Dragon reference. The pattern is achieved when the rotation angle is 45 degrees, creating intersecting lines that still function on the pattern as a single curve

3. When the angle of rotation is greater than 45 degrees the pattern ceases to function as a regular fractal curve 

4. The strategy of combining 3 different angles of rotation in one single line does not cause a disfuncion on the fractal pattern while maintaining the rule of not having any rotations on a angle greater than 45 degrees

5. The curve with the best ratio of length within the determined inicial curve is Iteration 08, with rotations on 45, 45 and 5 degrees respectively

6. Iterations made from polylines as the initial curve to be deformed instead of a straight line were conducted, but did not achieve a successful outcome

7. Iterations made from arches as the initial curve were also conducted and were not able to achieve an linear  fractal pattern 

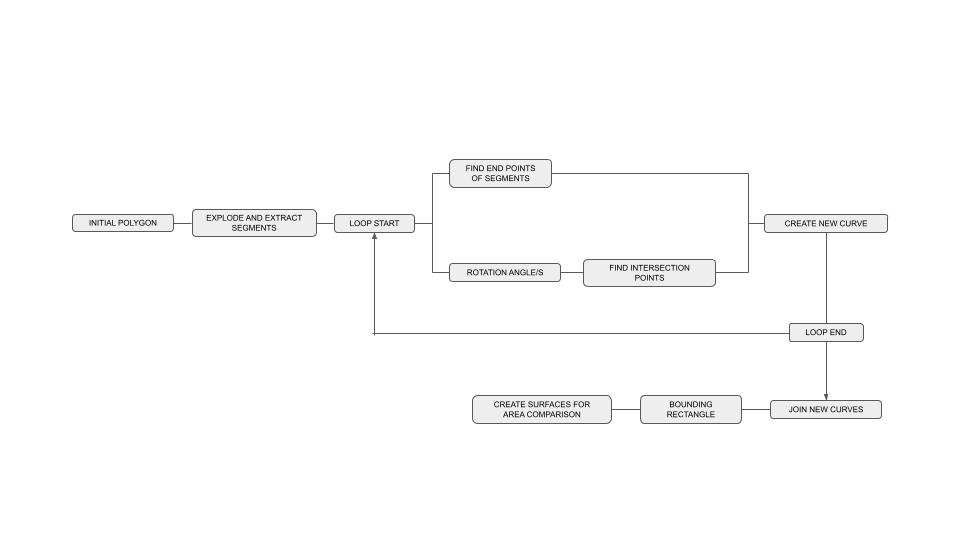
Research Exploration 02 – Polygons Fractals 

Goal: To explore different iterations of the fractal pattern when derived from a polygon 

Variable Parameters

1. Angle of rotation – single variation
2. Angle of rotation – 3 variations within the same pattern 

Non Variable Parameters:

1. Starting polygon 
2. Number of divisions within the curve 
3. Number of iterations 

Data Collected:

1. Initial Polygon perimeter length
2. Fractal perimeter length
3. Initial Polygon area 
4. Fractal  area 
5. Ratio of occupation within a defined boundary square

Polygons Iterations Catalogue

Conclusions on Polygons Iterations

1. The bigger the angle of rotation as the variable parameter, the bigger perimeter length is, creating a more “ramificated” curve. Meaning, there is an exponential growth proportionally related to the angle of the rotations

2. The area of the occupation on the other hand does not increases proportionally with the increase of the angles of rotation. 

3. It seems that the polygons with the smallest perimeter length have the bigger occupational porcentage. This could mean that the more a polygon contains ramifications, the smaller is its occupation of the square.

4. Polygons generated if only 45 degrees rotations or greater angles start to present intersections within itself

5. A surface can still be generated from a polygon containing a 55 angle rotation in its composition, but not greater than that. The Iteration that contains a rotation of 65 degrees in its composition failed to generate a closed polygon

Iterations Animations