
Fractals are commonly found within nature. They are self-similar structures, where one aspect of the fractal is identical to the rest. This allows it to be scaled up or down while fitting within itself.
Within trees, fractalization is found in the way the branches are grown from each other, always yielding smaller and smaller versions of itself, starting with the trunk.


__________________________________________
L- Systems: Trees
Four different species of trees were chosen based upon two factors; the first being the type of fractalization that occurs within the branches. The second being the rates of growth per year experienced by the tree.




__________________________________________
Tree Growth with Fractals
As the tree grows, the mother branch (the trunk) produces two daughter branches, which then produce more of themselves as the tree gets older.
This fractalization can be replicated within mathematics through the use of L-systems.
__________________________________________
L- Systems
An L-System is an “alphabet of symbols that can be used to make strings; a collection of production rules which expand each symbol into some larger string of symbols”
They are used to make fractals and self-similar systems.
To make them you need an alphabet (symbols), a starting point (axiom), and a rule.
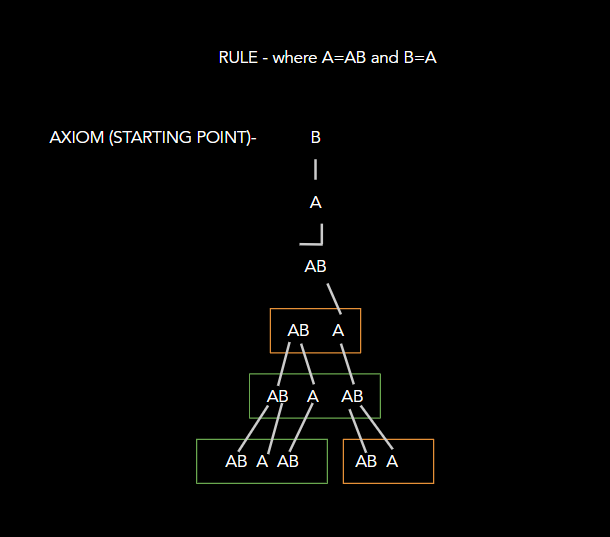
The system starts with the Axiom word. This word is then what is repeated X amount of times (in this case 17 as seen below). The axiom word, however, responds to the rules that make up the letters within it. In this case only A and B are used. So A has a specific code created by the alphabet and so does B. These are then used to create the starting “word” these codes are then followed within the repetitions adding to themselves over and over, creating the L-system and self-similar parts. ( see above diagram )

This alphabet was used to create different “words” used to draw the fractal branches.
The components made by creating systems for each of the alphabet letters was used as a way to firstly, understand the way they work in 2D and 3D, but then later to try to piece together to make a fractal branch. This later was only used as a way to visualize the alphabet, as the components became increasingly complicated to use within a grasshopper script.
__________________________________________
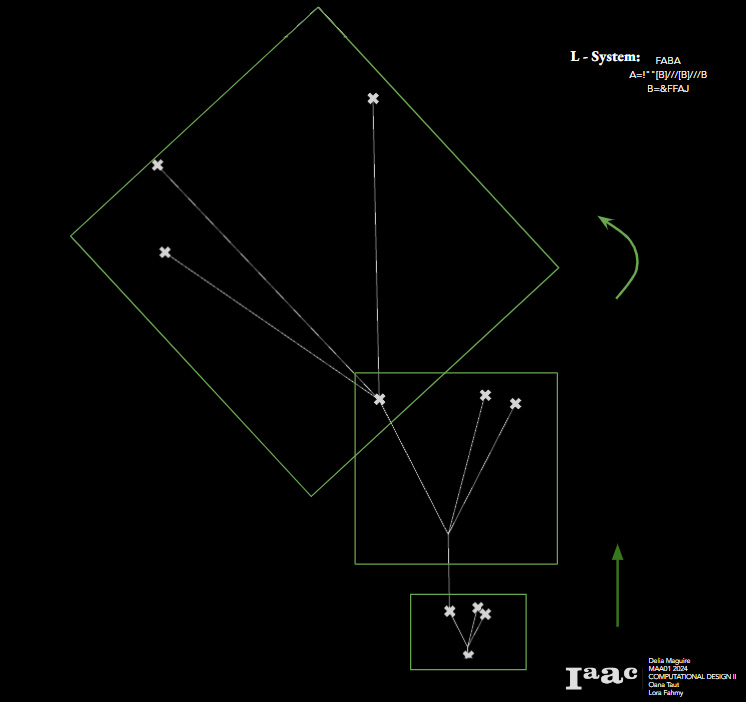
L- Systems: First Attempts

__________________________________________
L- Systems: Tree Catalogue

Each “word” created from the alphabet was then repeated 17x to create the trees that are seen above.

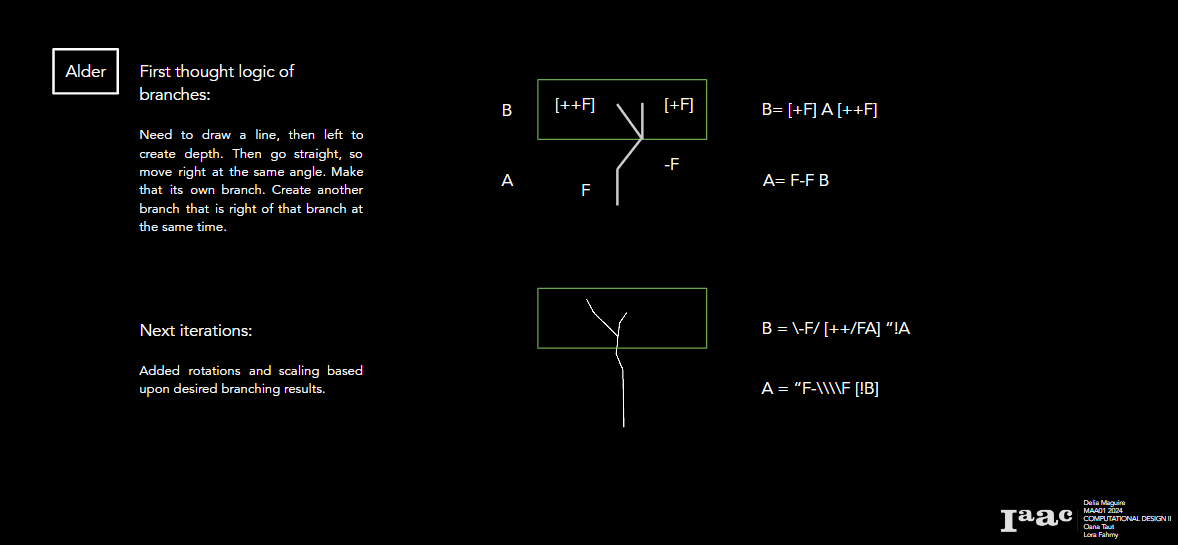
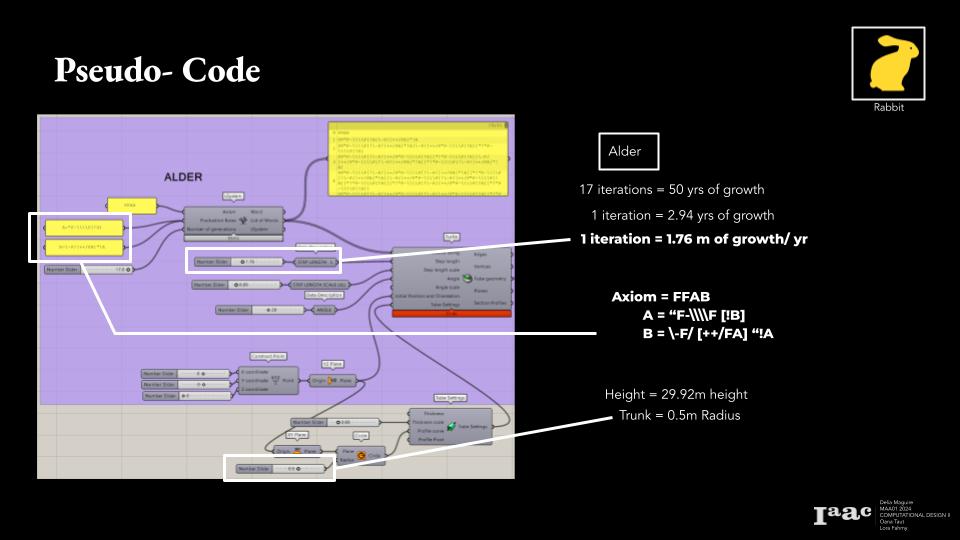
Alder Tree
FFAB
A = “F-\\\\F [!B]
B= \-F/ [++/FA] “!A

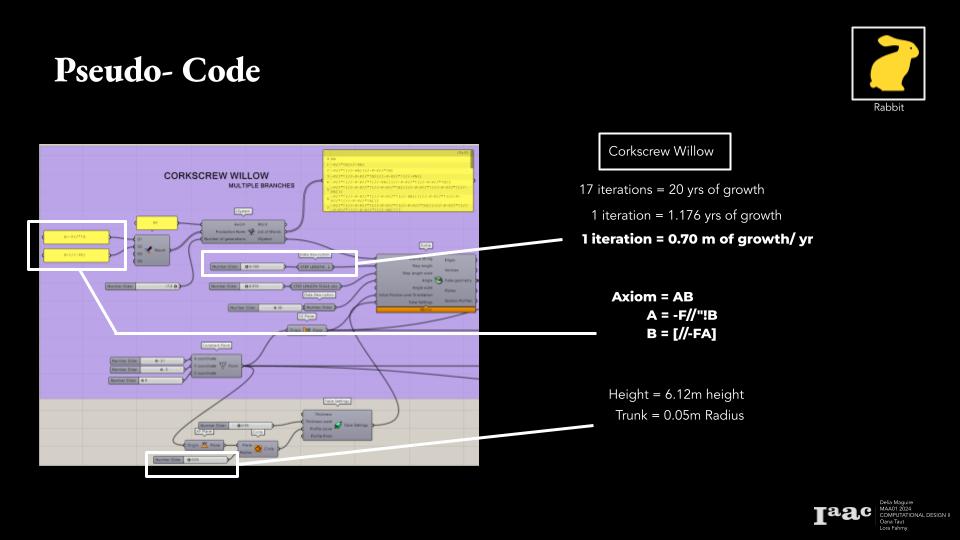
Corkscrew Willow Tree
AB
A = -F//”!B
B = [//-FA]

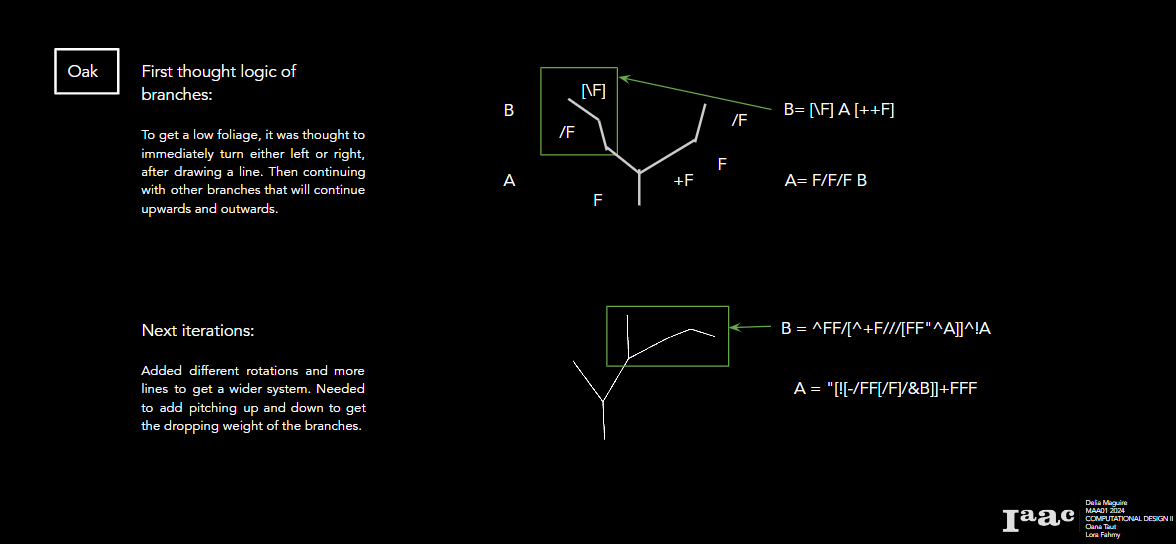
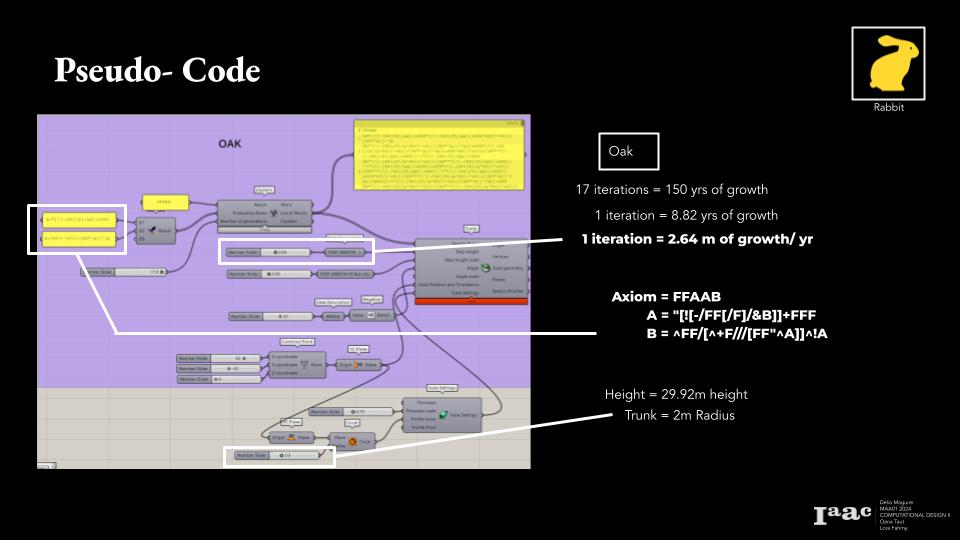
Oak Tree
FFAAB
A = “[![-/FF[/F]/&B]]+FFF
B = ^FF/[^+F///[FF”^A]]^!A
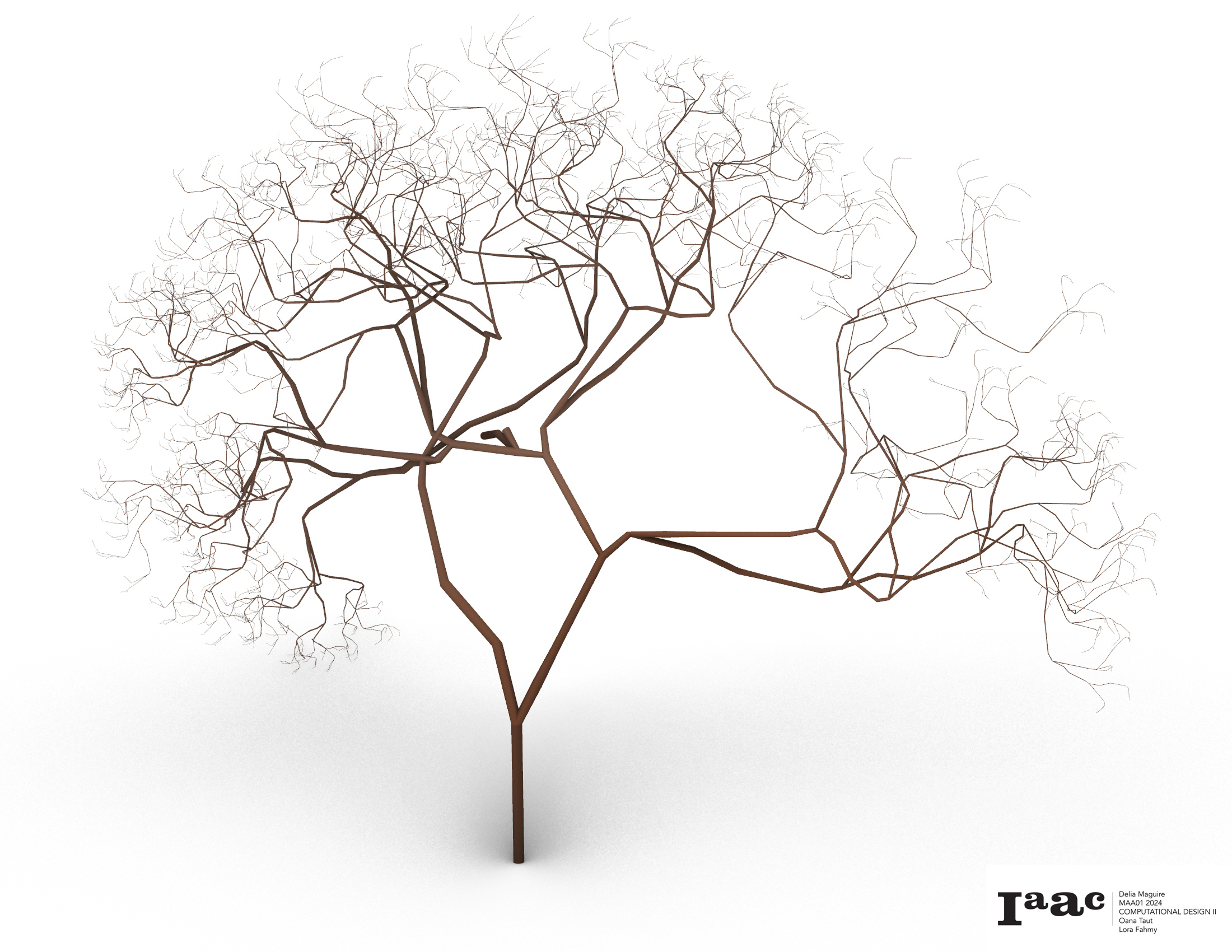
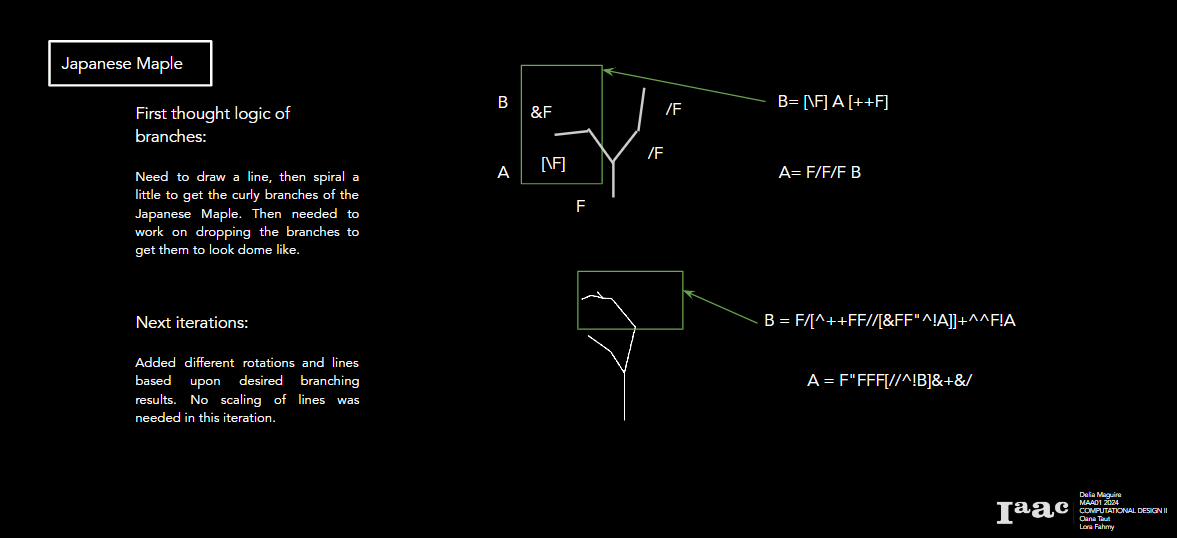
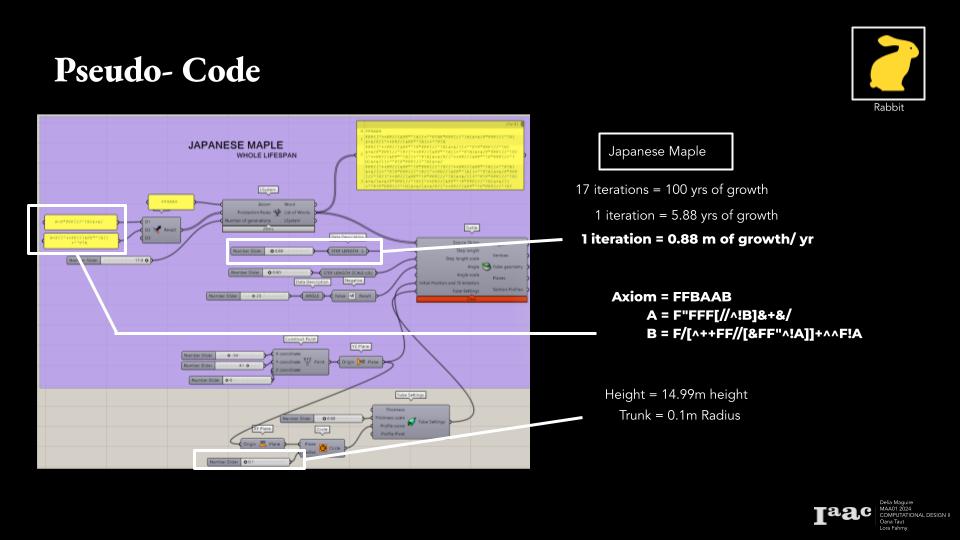
Japanese Maple Tree
FFBAAB
A = F”FFF[//^!B]&+&/
B = F/[^++FF//[&FF”^!A]]+^^F!A
__________________________________________
Tree Growth Rates
The second factor in deciding which species of trees to work with was the different rates of growth per year. Different species of trees grow at different rates, yielding different heights, patterns and branch widths.
Two trees chosen to represent the fast growth trees, Alder and Corkscrew Willow, both grow at 60cm/year.
Two trees chosen to represent the slow growth trees were the Oak, at 30cm/year and Japanese Maple at only 15cm/year.

The rates of growth were used to calculate the years between each iteration. Iterations had to be capped at 17 iterations of the L-System, due to the heaviness of the system.
__________________________________________
Pseudo-Code
L-systems can be made within grasshopper with the anemone or the rabbit plugin.
Anemone works with more manual aspects, needing to move and rotate the original line through commands, while rabbit works solely with the L-system alphabet explained above.
For this reason, exploration began with anemone, learning the different letters of the L-system alphabet manually, and continued to the rabbit plug-in for more complex structures, as anemone became difficult in achieving larger codes.
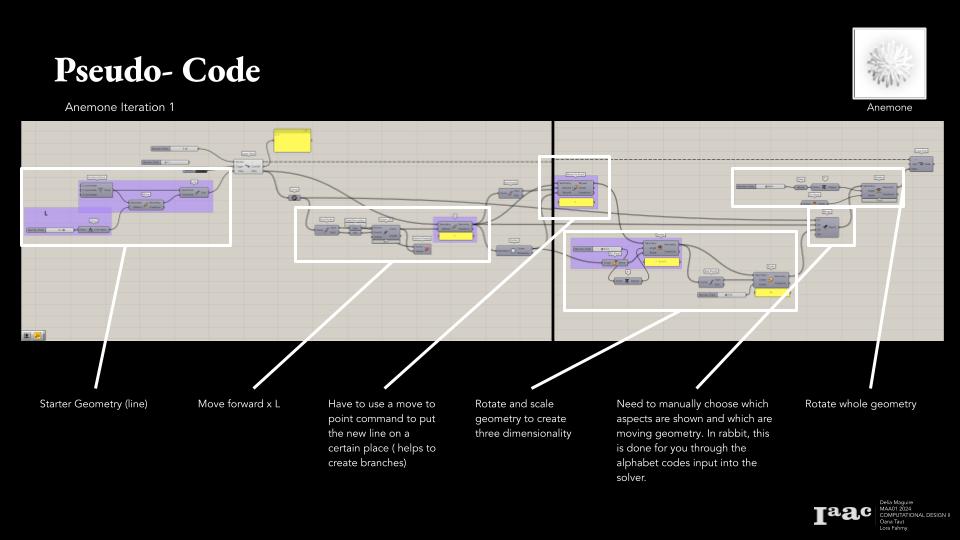


Since it was harder to get more complex results, anemone was abandoned and rabbit was used.
__________________________________________
Tree Growth Rates
The rates of growth were used to calculate the years between each iteration. Iterations had to be capped at 17 iterations of the L-System, due to the heaviness of the system.
This rate if growth was then used as the L component or the Step Length for each line. With this, the proper heights were achieved.

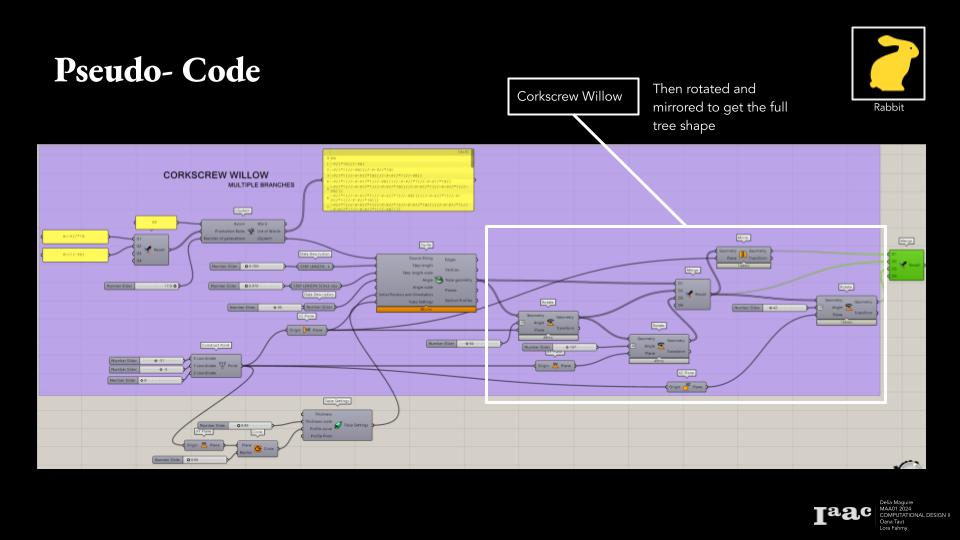
These heights and calculated growth was then plugged into the Rabbit plugin along with the axiom and defining words from earlier. This whole system created the tree branching and thus created the tree.
__________________________________________

