Introduction – Hypothesis
How can we optimize the geometry of different sections of a 3D-printed wall to adapt to varying levels of solar radiation and insulation requirements, while also reducing material usage and printing time?
By deforming the infill patterns of 3D-printed earth walls, it is possible to optimize the thermal transmittance of the walls, resulting in more energy-efficient building and a reduction of the printing time and material.
Why is isolation important?
Presently housing constitutes 40% of the total energy demand from EU. “Adobe as a Sustainable Material: A Thermal Performance”
Homeowners can save an average of 15% on heating and cooling costs by air sealing their homes and adding insulation.
U-Value as a Evaluation Criteria
Thermal transmittance, also known as U-value, is the rate of transfer of heat through a structure. The units of measurement are W/m²K. The lower the U-Value the better the isolating properties of the material
Calculation:
U-Value = 1 / (Rse + R1 + R2 + Rsi)
Rx = Thickness / Conductivity
Examples:
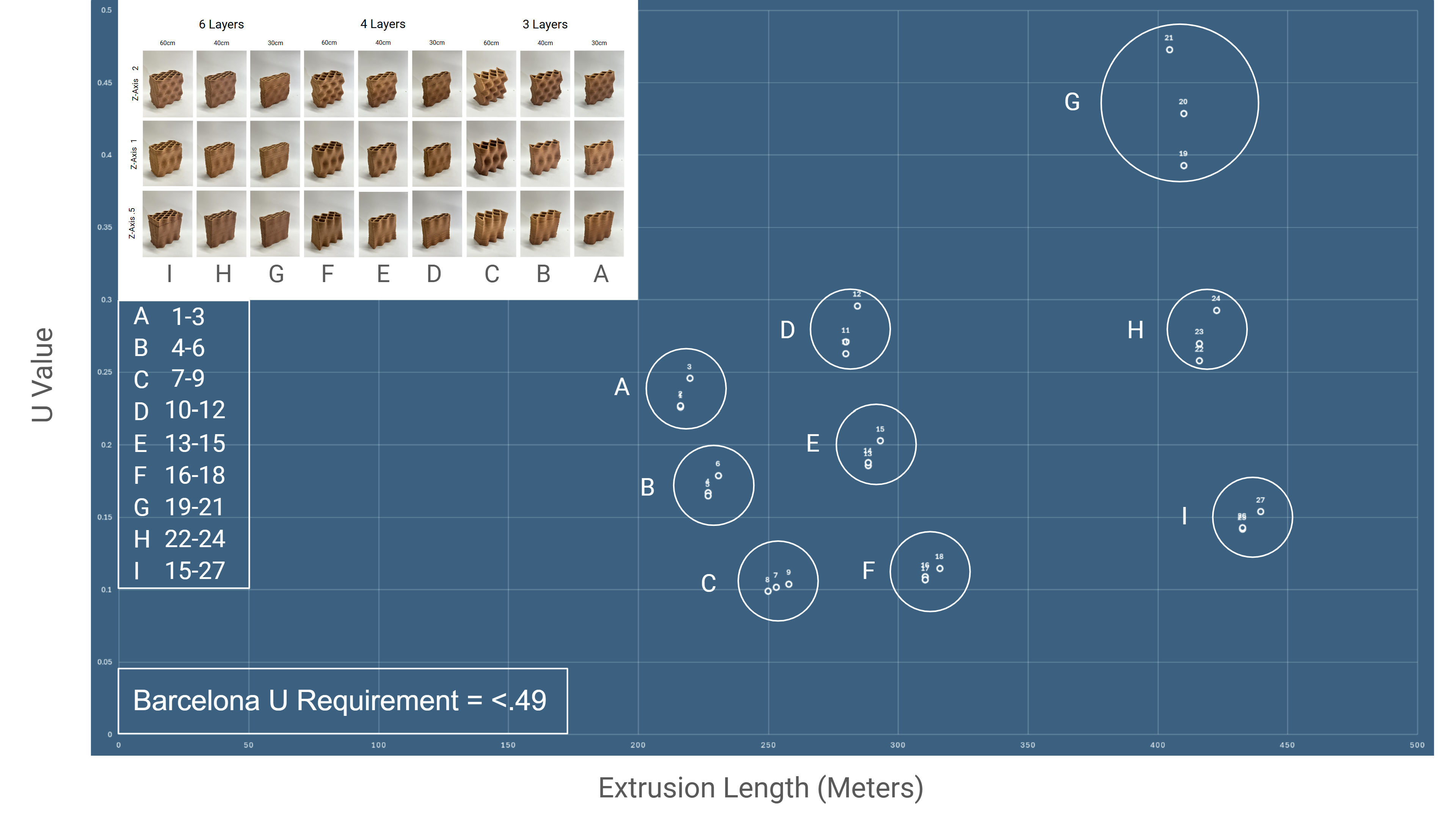
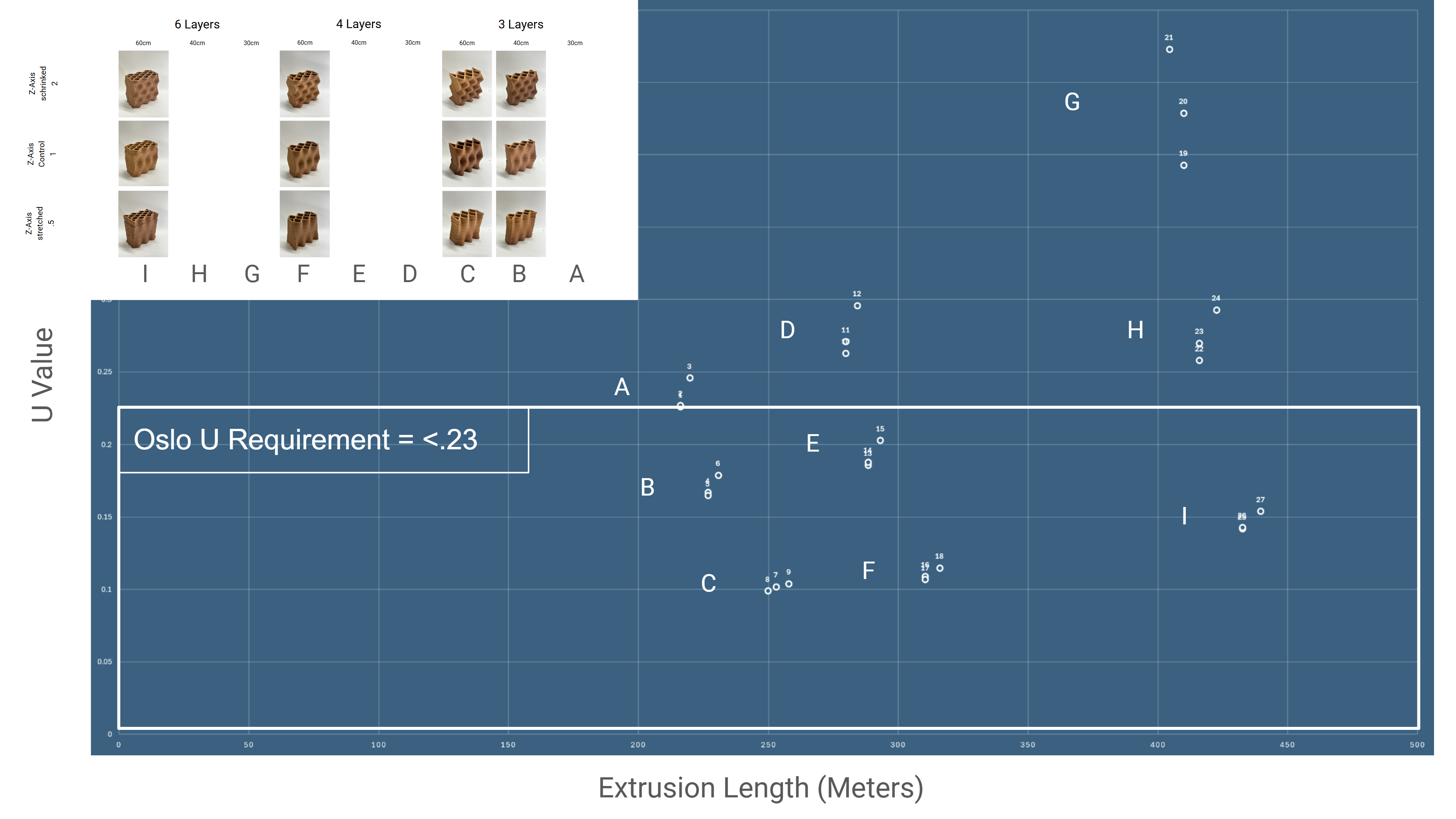
According to the CTE in Barcelona, the U-Value for a Facade wall should be below 0,49 W/m²K and below 0,23 W/m²K according to the TEK17 in Oslo, Norway.
Traditional Architecture vs. 3d Printing Architecture

Traditional Architecture advantages: Takes 1/7 of time to build the same wall
Traditional Architecture disadvantages: Higher U Value – Lower isolation
3d Printed Architecture advantages: Lower U Value (air cavities have a very low conductivity) – higher isolation
3d Printed Architecture disadvantages: Takes 7 times more to build the same size of the wall
3d Printed Architecture Analysis
This two different geometries of 3d Printed Walls have the same U-Value when the equation is applied but the percentage of contact surface area between the layers (thermal bridges) are very different.

Thermal bridge is an area or component of an object which has higher thermal conductivity than the surrounding materials, creating a path of least resistance for heat transfer

Alteration of U-Value Calculation for 3d Printed Architecture
U-Value = 1 / (Rse + R1 + R2 + Rsi)
Rx = (Thickness / Conductivity) x (Percentage of thermal bridge)

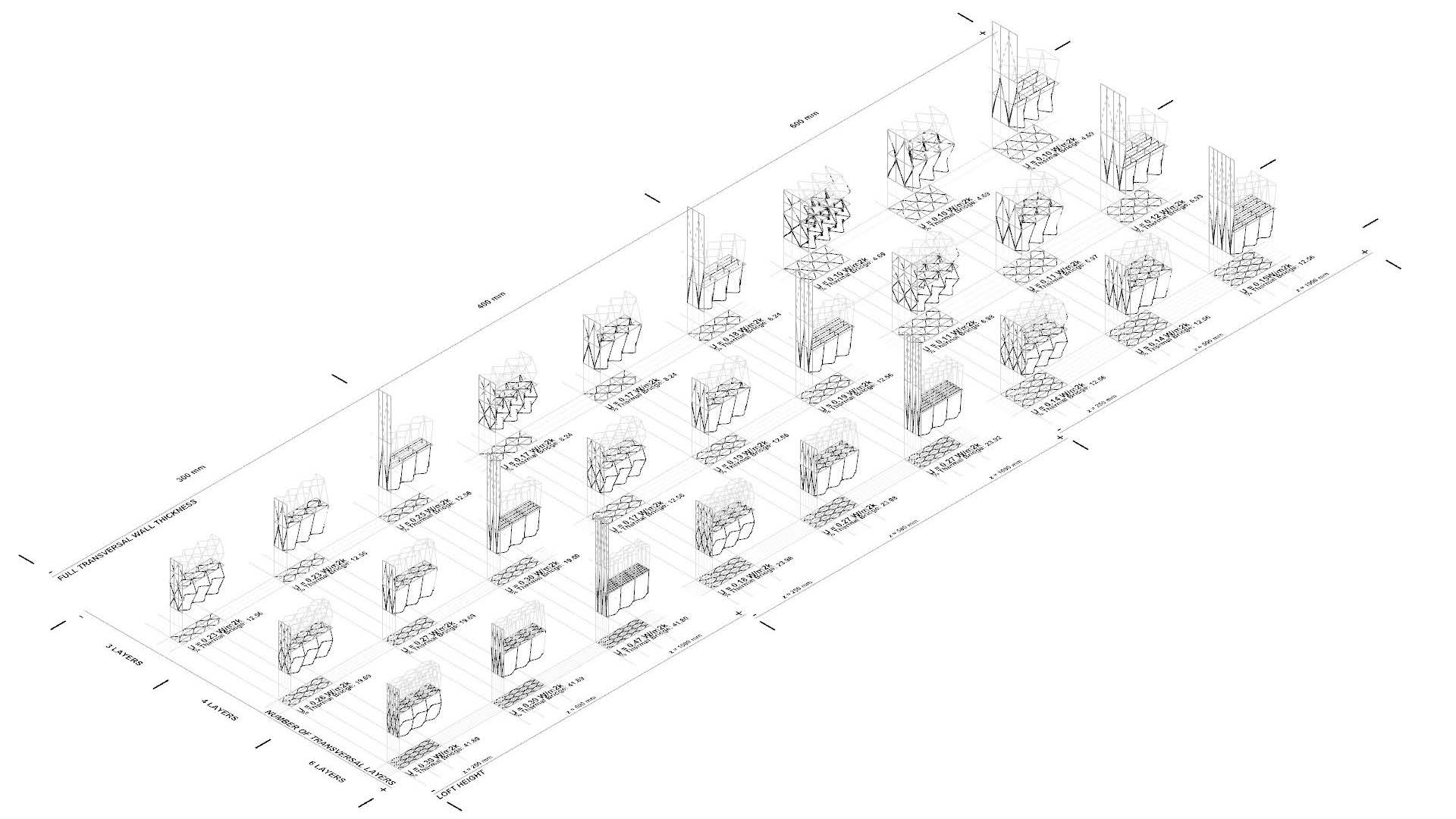
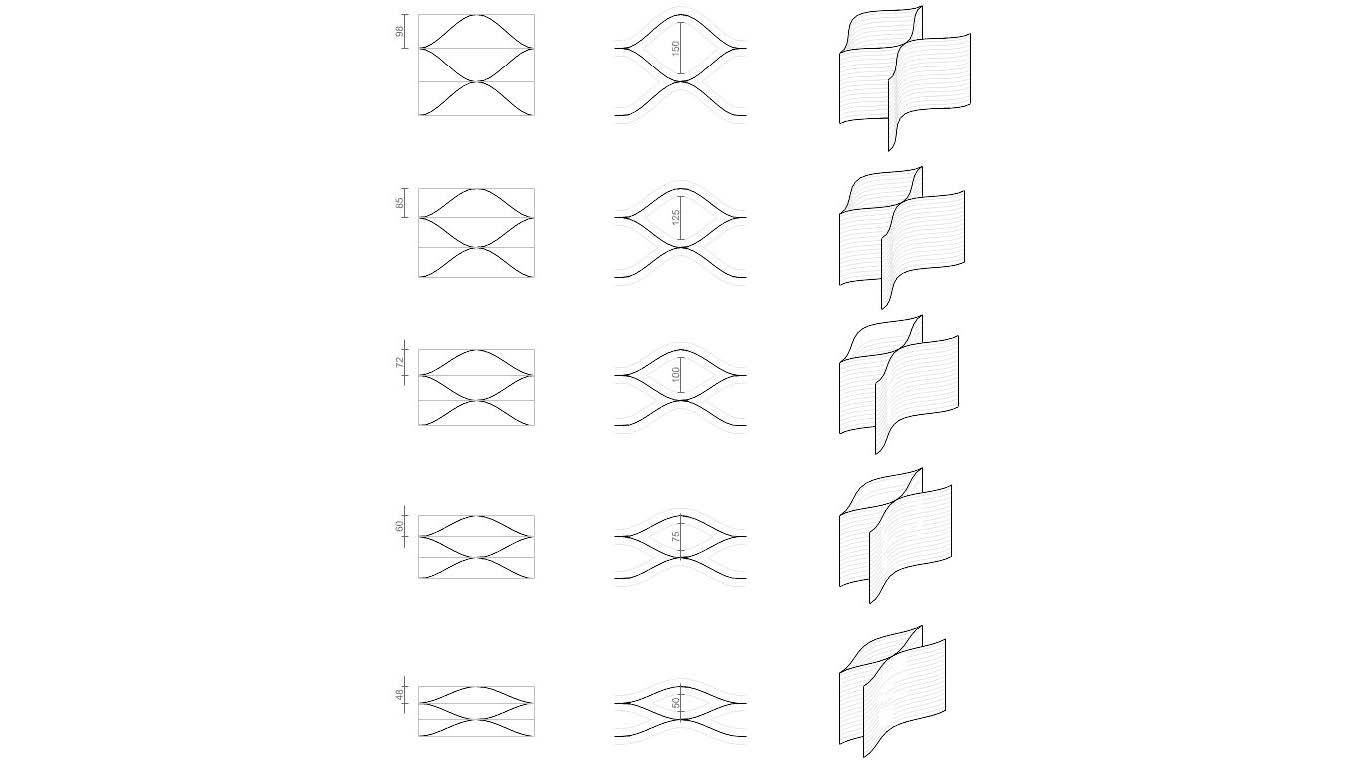
Deformation Parameters chosen for a Period
These selected deformations are all applied to the same period. We believe that all these results extracted of these deformations could also be applied to other periods
Transversal axis – Z axis – Number of layers
Transversal Axis Approach

Transversal and Z axis deformation approach
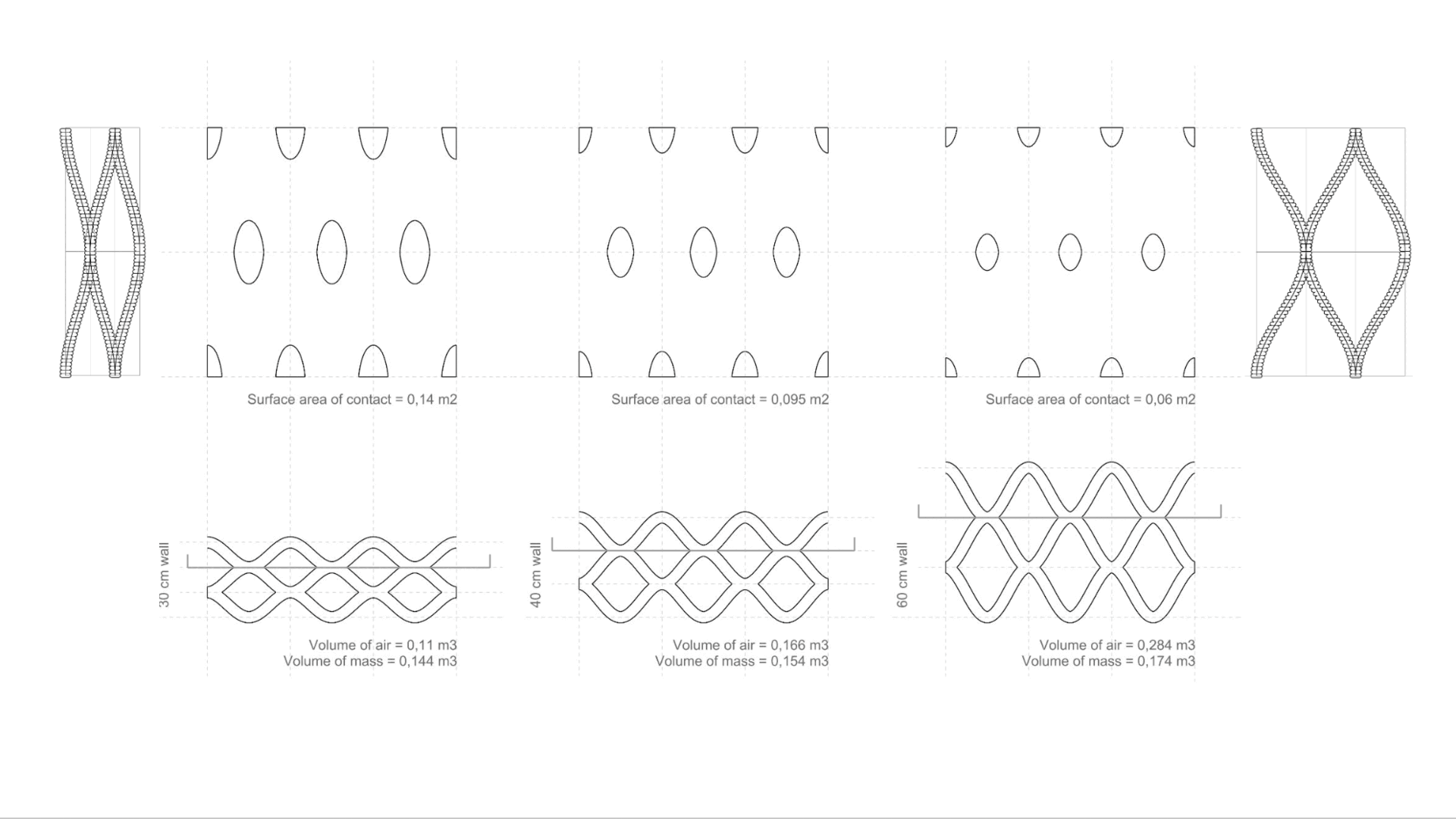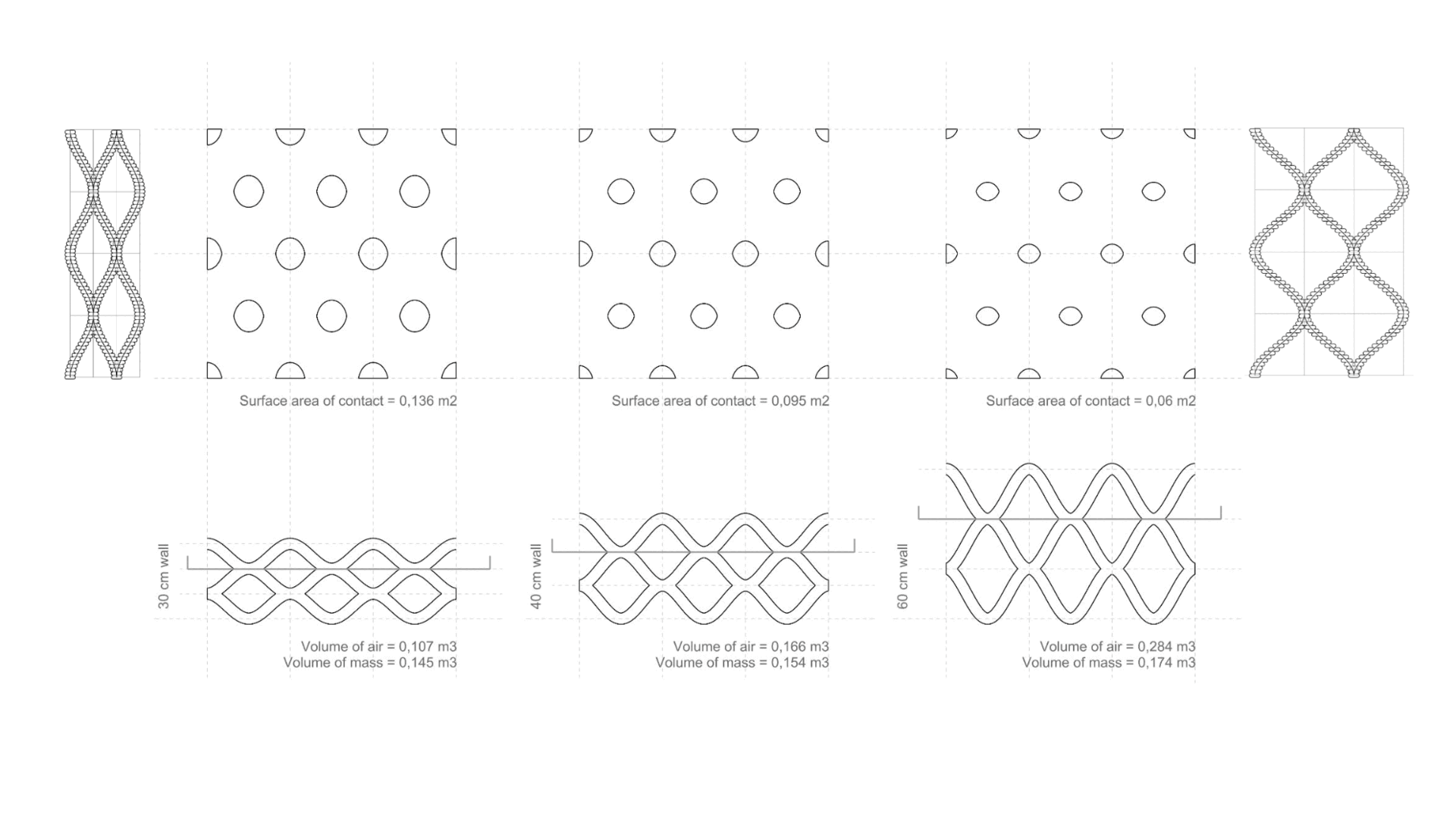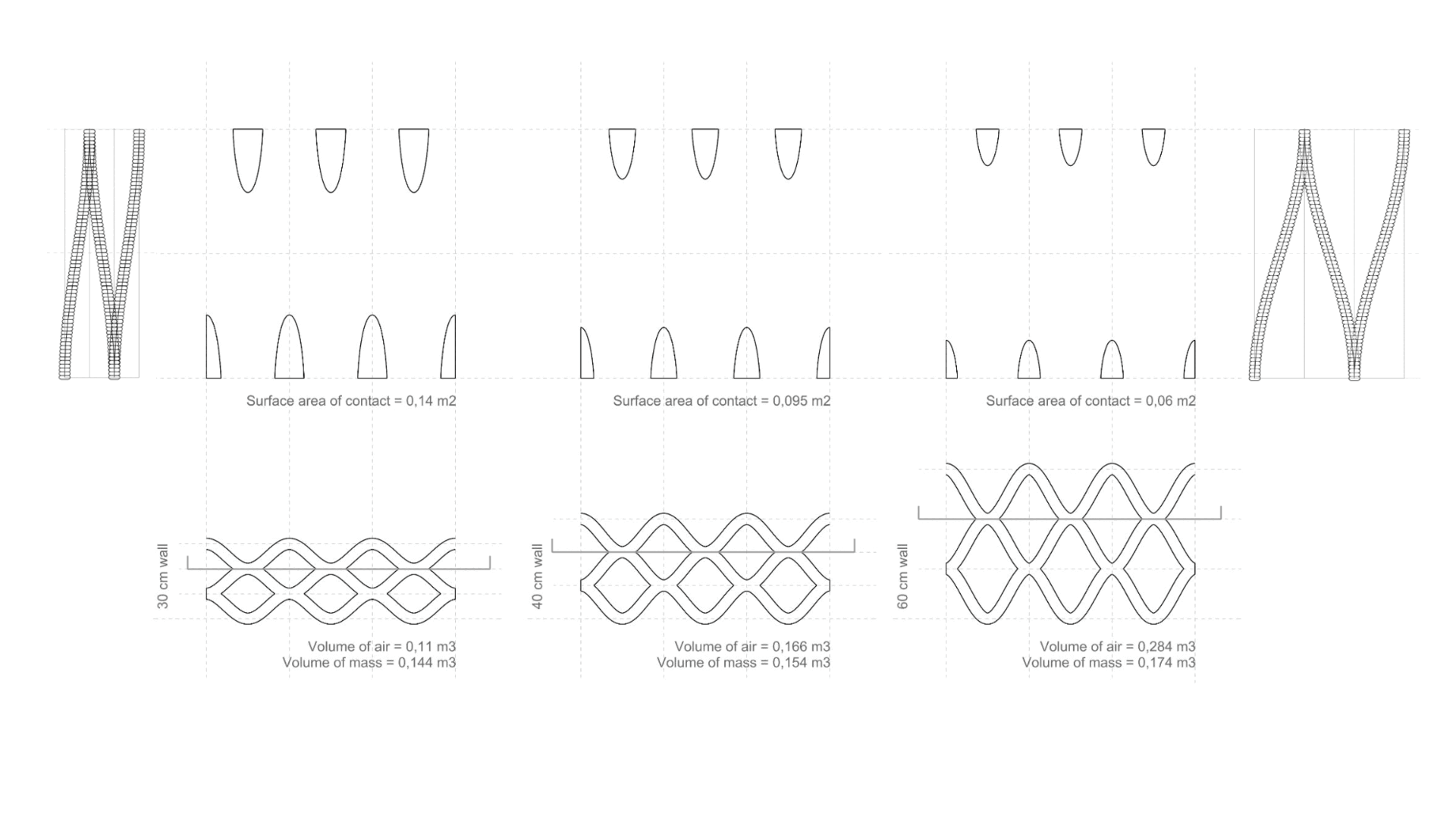
Complete Catalogue/Matrix

The Performative Wall
Different parts of a wall are exposed to different variables. Therefore, different parts of the same wall need to respond and perform differently.
Applying a combination of the previously tested deformations gives rise to The Performative Wall, deformed uniquely and not uniform throughout.
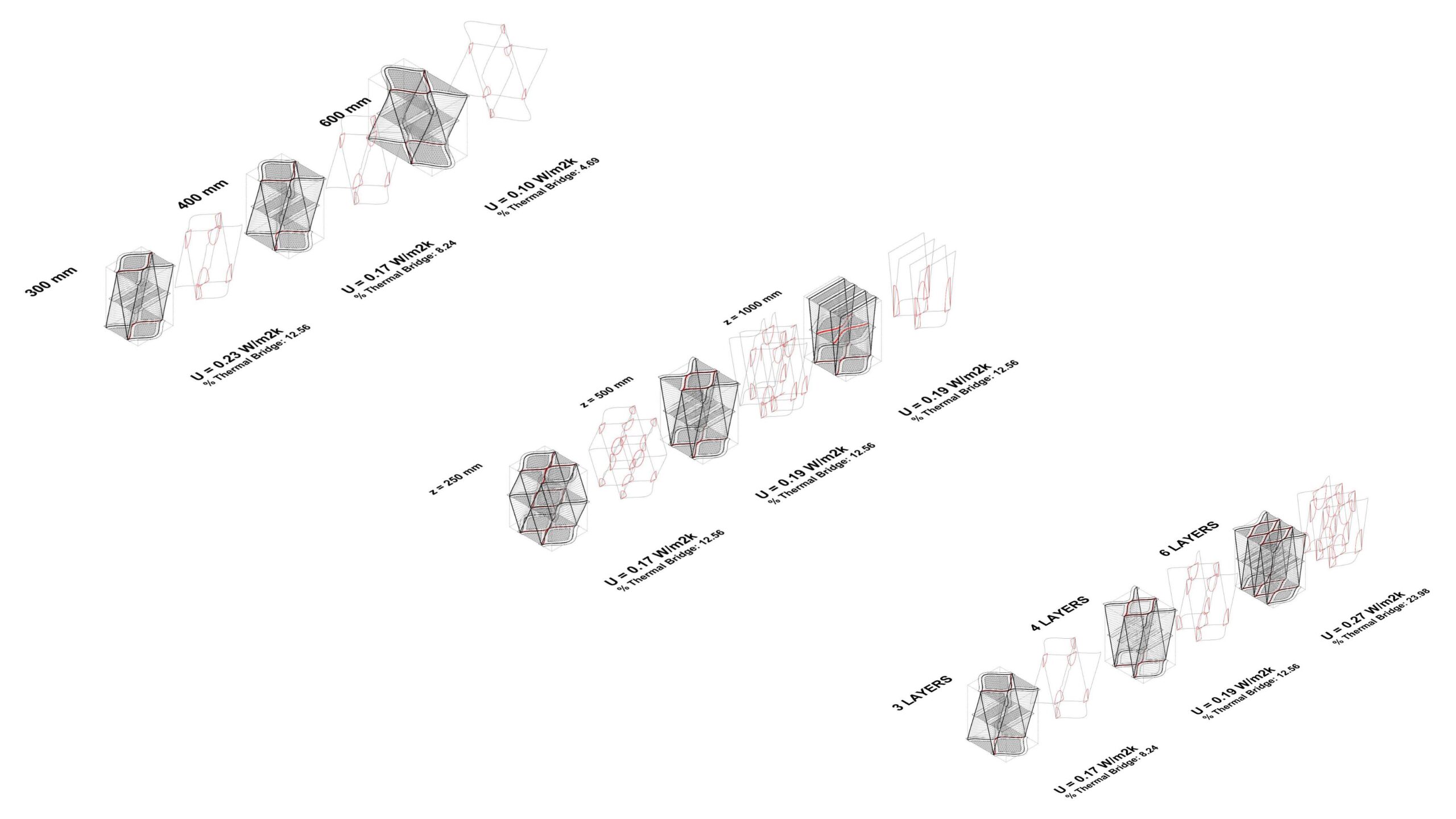
Above, the three types of deformation and the resulting effect on “U value” and “% Thermal Bridge” (contact points) are highlighted. The group in the top left shows transversal deformation. In the middle, deformation across the Z axis. Lastly, on the right, deformation through the addition or subtraction of layers. This digital evaluation allows for the toolkit to evaluate any given period and a family of variations so each may evaluated for performance and construction advantages.
Digital Analysis Results
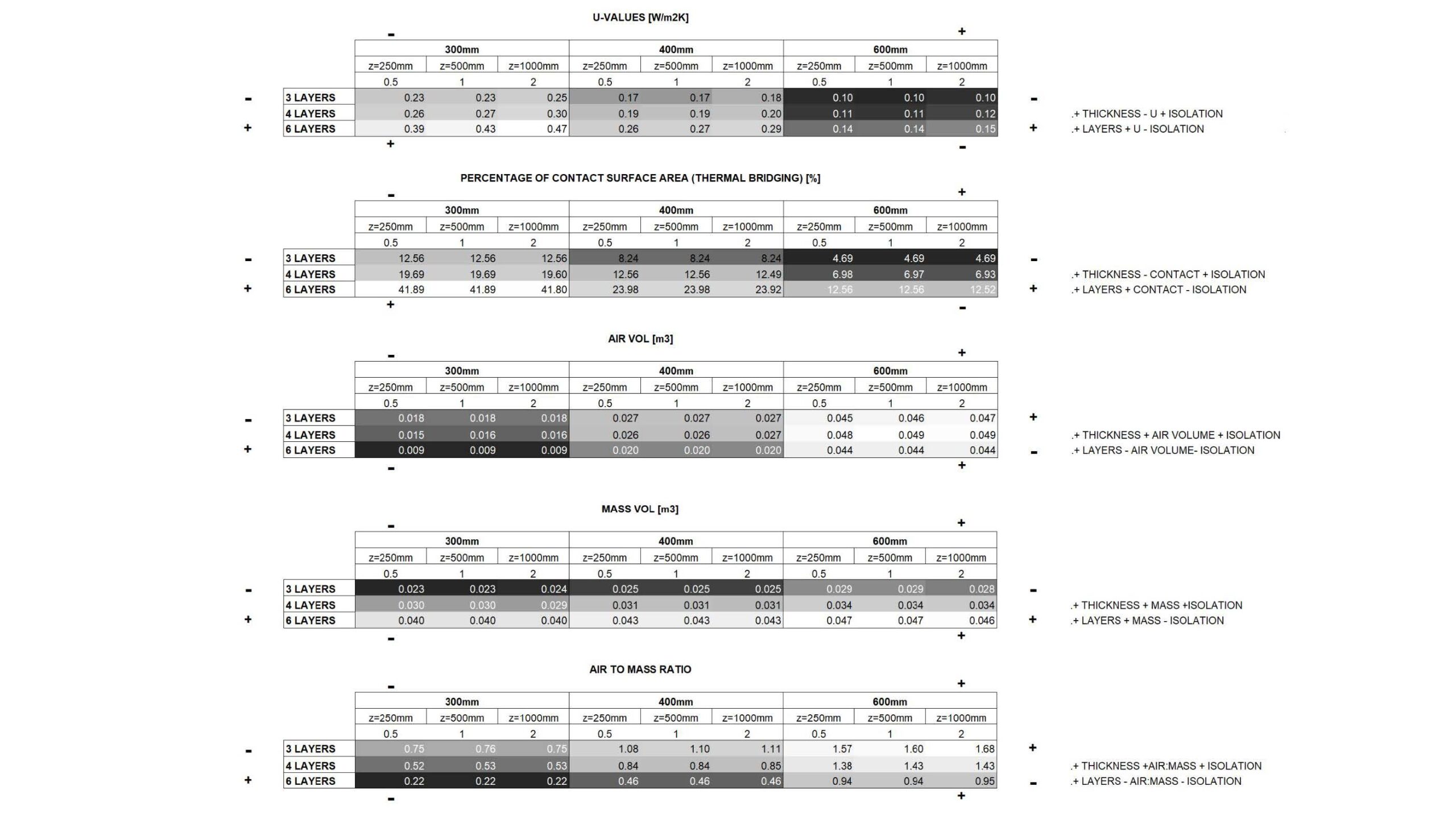
DIRECTLY PROPORTIONAL
CONTACT, U, LAYERS
AIR VOLUME, MASS
MASS, THICKNESS, LAYERS
INVERSELY PROPORTIONAL
U & ISOLATION
CONTACT & ISOLATION
THICKNESS & U
THICKNESS & CONTACT
Matrix of Physical Testing
Printed Matrix – 1:10 (10mm x 10mm x 30/40/60mm)

Physical Testing
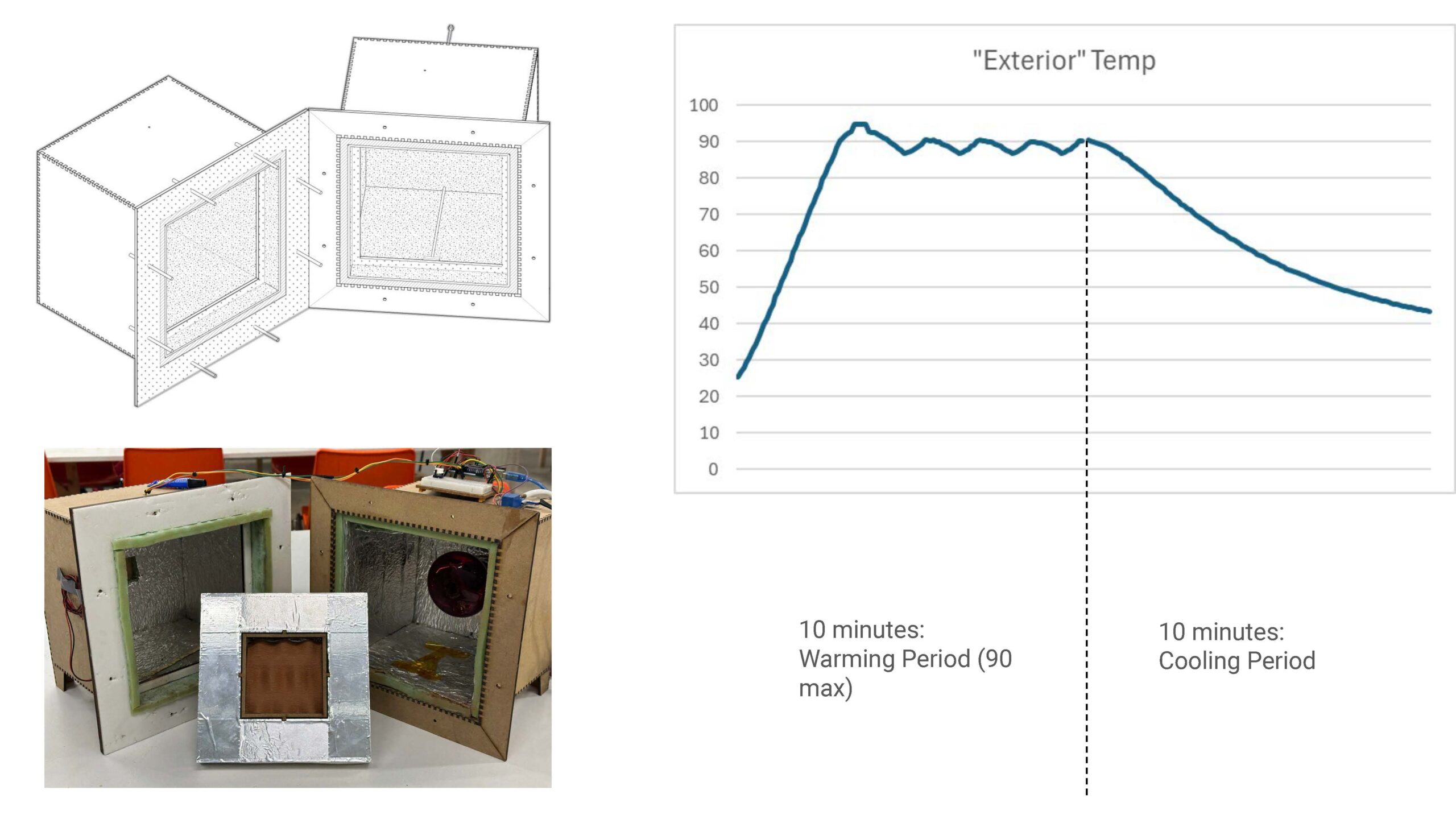
The physical testing consisted of a 20-minute cycle for each print in the matrix. The wall divides the heating chamber into two spaces, representing an interior space and an exterior condition with sensors integrated to record temperature change. The “exterior” is heated to 90°C and maintains this temperature for 10 minutes. Once this first cycle is completed, the heat source turns off, dissipating heat through the wall. This test was designed to evaluate the isolation potential of each print (phase 1) and how much energy is stored and released from the material (phase 2).
Constant: Z deformation
Conclusion: Higher mass results in a slower distribution of heat, the volume of air doesn’t have a large impact at this scale.
Future steps: Perform tests of full-scale periods to better understand the impact of air cavities on isolation.
Constant: Wall thickness
Conclusion: The largest differences are observed between the 3 and 4-layer walls. Little difference can be seen between 4 and 6-layer walls. This trend means we could consider eliminating 6 layers due to how much material is required for such little impact on performance.
Future steps: Extend the time of tests a heating rate more closely related to real-world conditions and provide a longer period of time to observe the distribution of heat in phase 2 of the test to more accurately observe heat diffusion (lag).
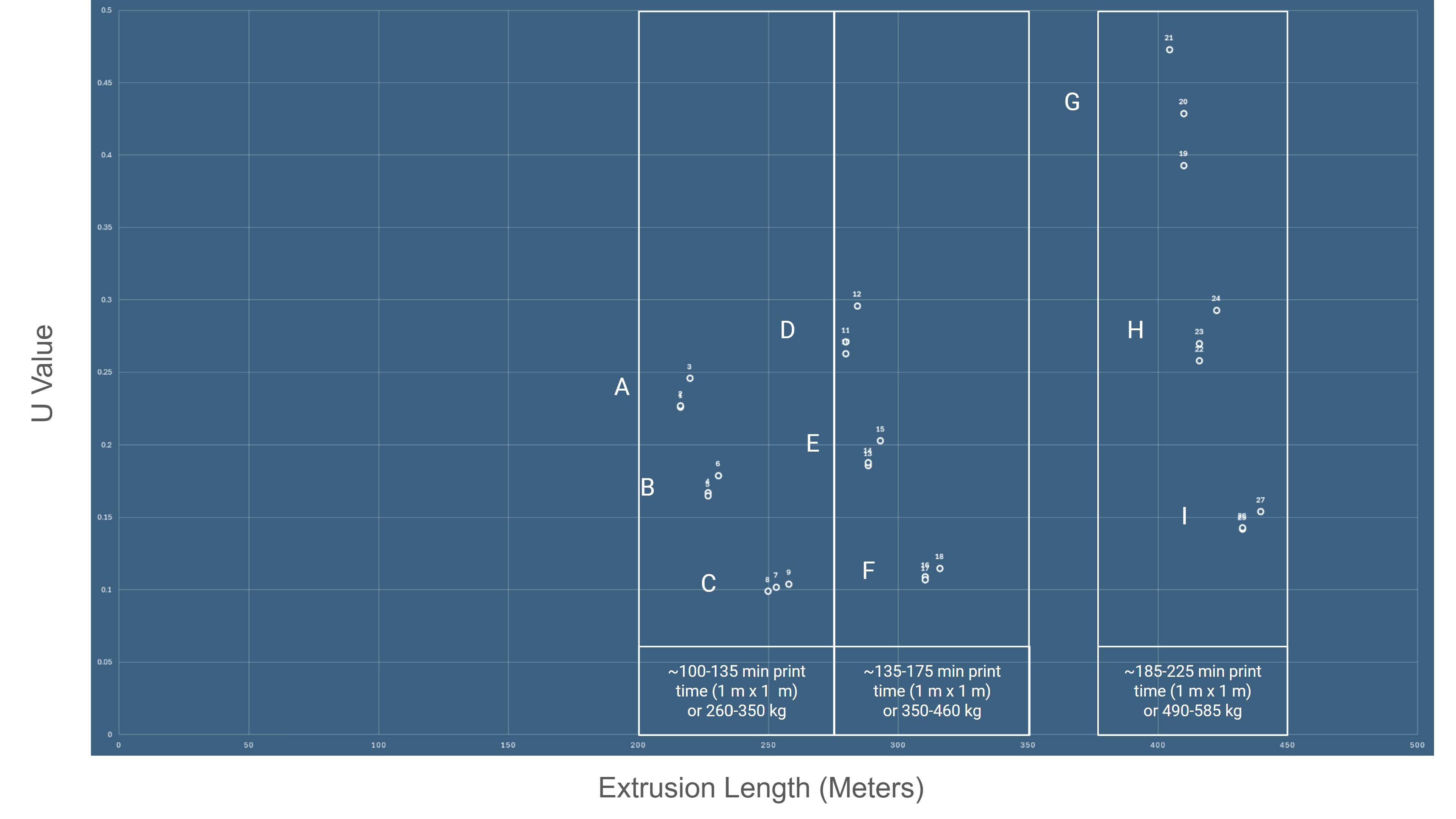
Selection Matrix
The following charts compare the results of the digital analysis for the 1:1 versions of our matrix. This provides a tool for future construction to analyze the best range of period deformations to apply for any given climate and construction constraints.
Future Tests
To validate the digital hypothesis, 1:1 scale physical testing is essential. It is understood that the performance of a given air cavity becomes obsolete after a certain thickness. This proposed model would allow for confirmation of how much air cavities can deform while still enhancing insulative properties. Furthermore, a more accurate performance metric can be determined, strengthening the resulting charts and selection tools.
The Toolkit
The toolkit follows the hypothesis that currently, 3D printed walls are over-designed and over-performing. The output of the toolkit minimizes over-designing for over-performance, maintaining optimal performance while reducing time and material.
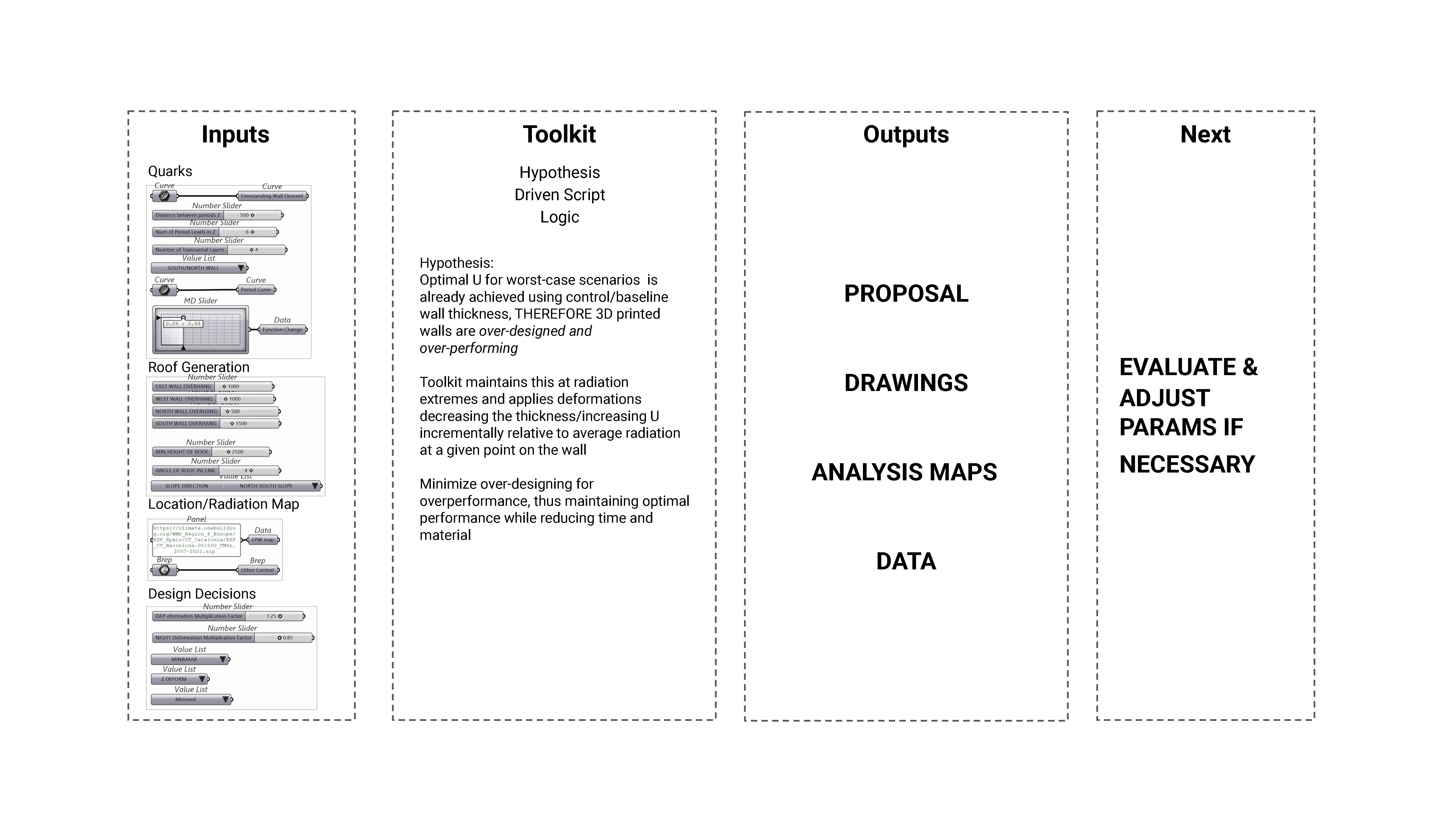
Inputs include a base perimeter curve, period curve, desired height of wall, orientation of the wall (N/W/S/E), location of programmatic change behind the wall, etc. Parameters for user adjustment are available for the roof generation for later solar incidence analysis. The toolkit asks for the location for radiation analysis. Design decisions such as multipliers for the deformations, different dispatch patterns (MIN/MAX & AVG/EXTREMES) are offered.
What is it? A tool which:
-Proposes optimized wall geometries relating thermal performance to efficiency and material conservation
-Calculates & Optimizes U-Values across the wall
-Produces Drawings, Analysis Maps, & Data tables documenting the wall’s performance and geometric generation
All following geometries, drawings, maps, calculations, & data are produced directly by the toolkit.
Pseudocode
The basic quarks of the toolkit are the perimeter curves of a given spatial design, which the toolkit generates a roof for before it begins analysis & geometry generation.
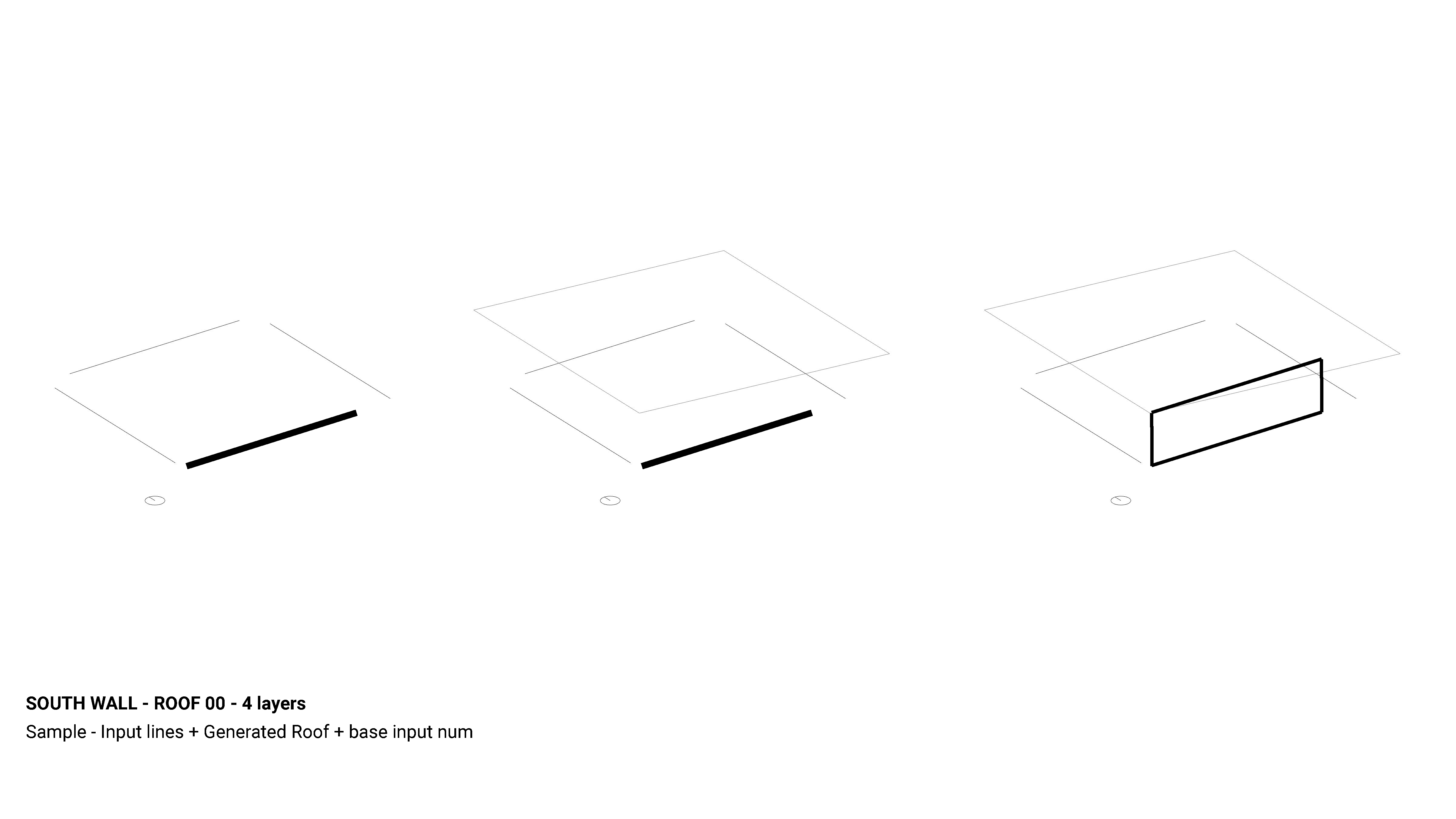
The wall is discretized for numerical analysis on each portion of the wall at two levels: 1 period x 1 period for evaluation of said portion of the wall, and zone surrounding deformation points, referenced here as crosses, for radiation data analysis.

The radiation analysis offers two dispatch directions: minimums and maximums, or averages and extremes, to be given different deformation criteria.
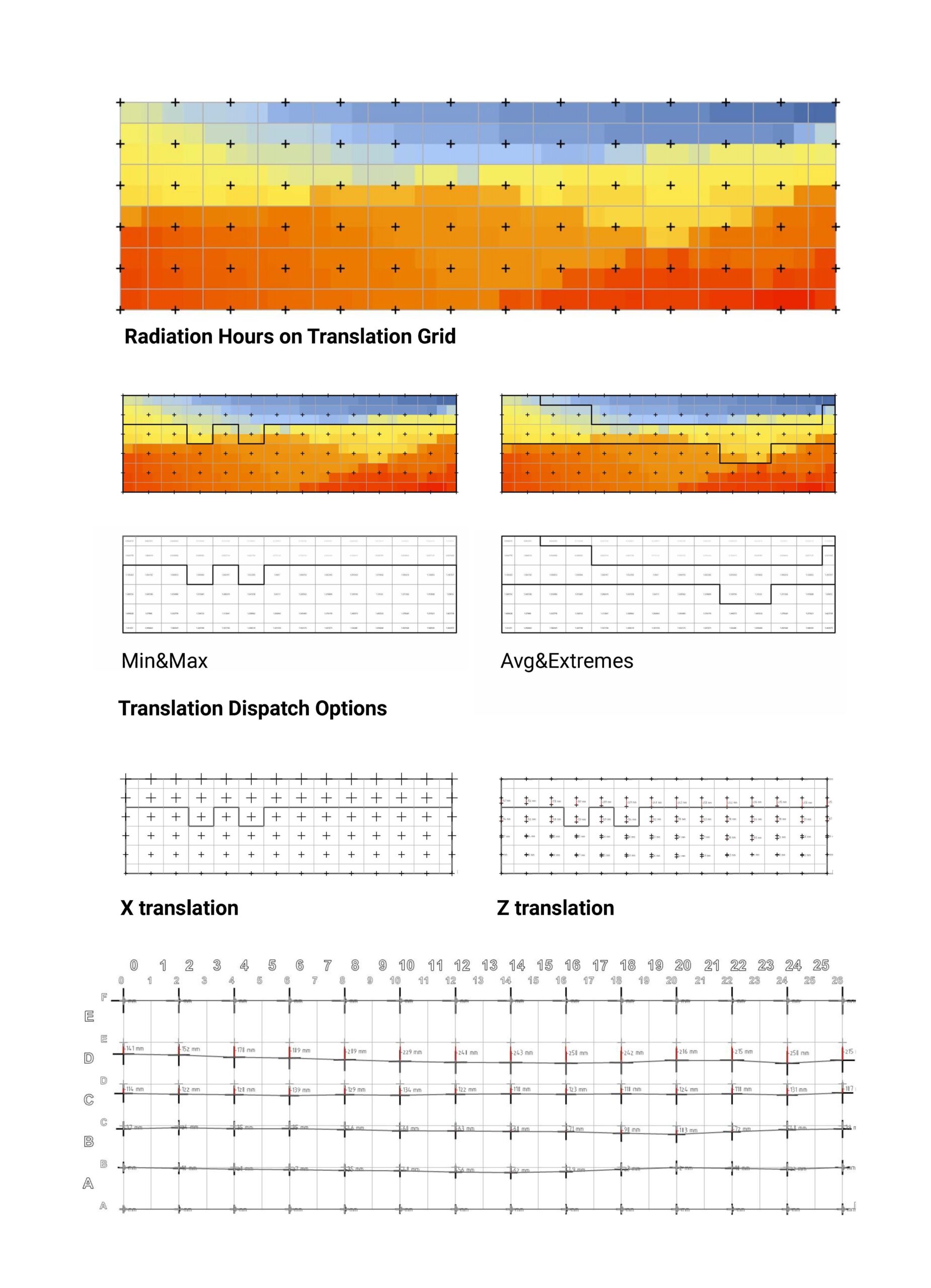
The deformations here were following the Min&Max dispatch option.
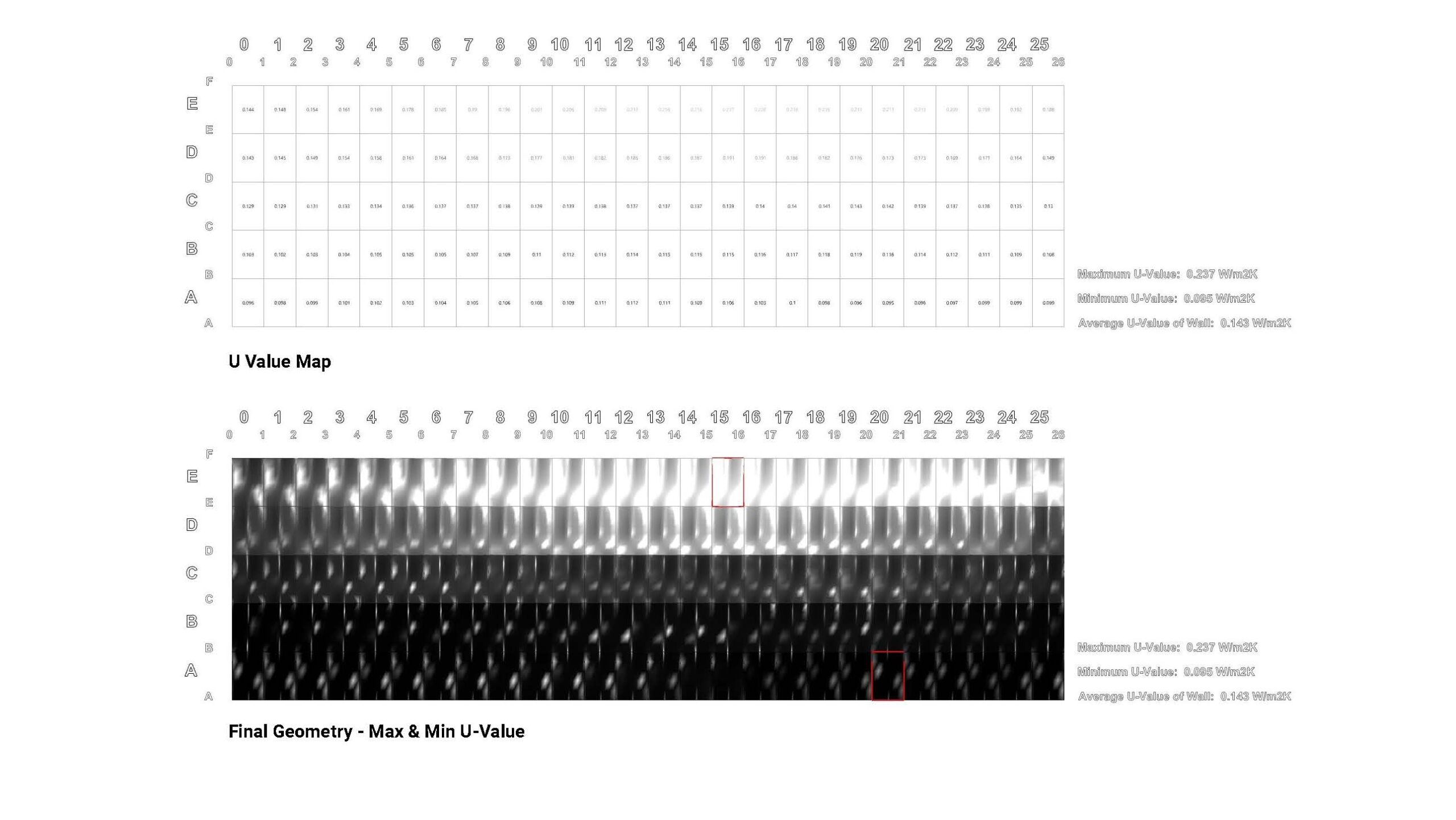
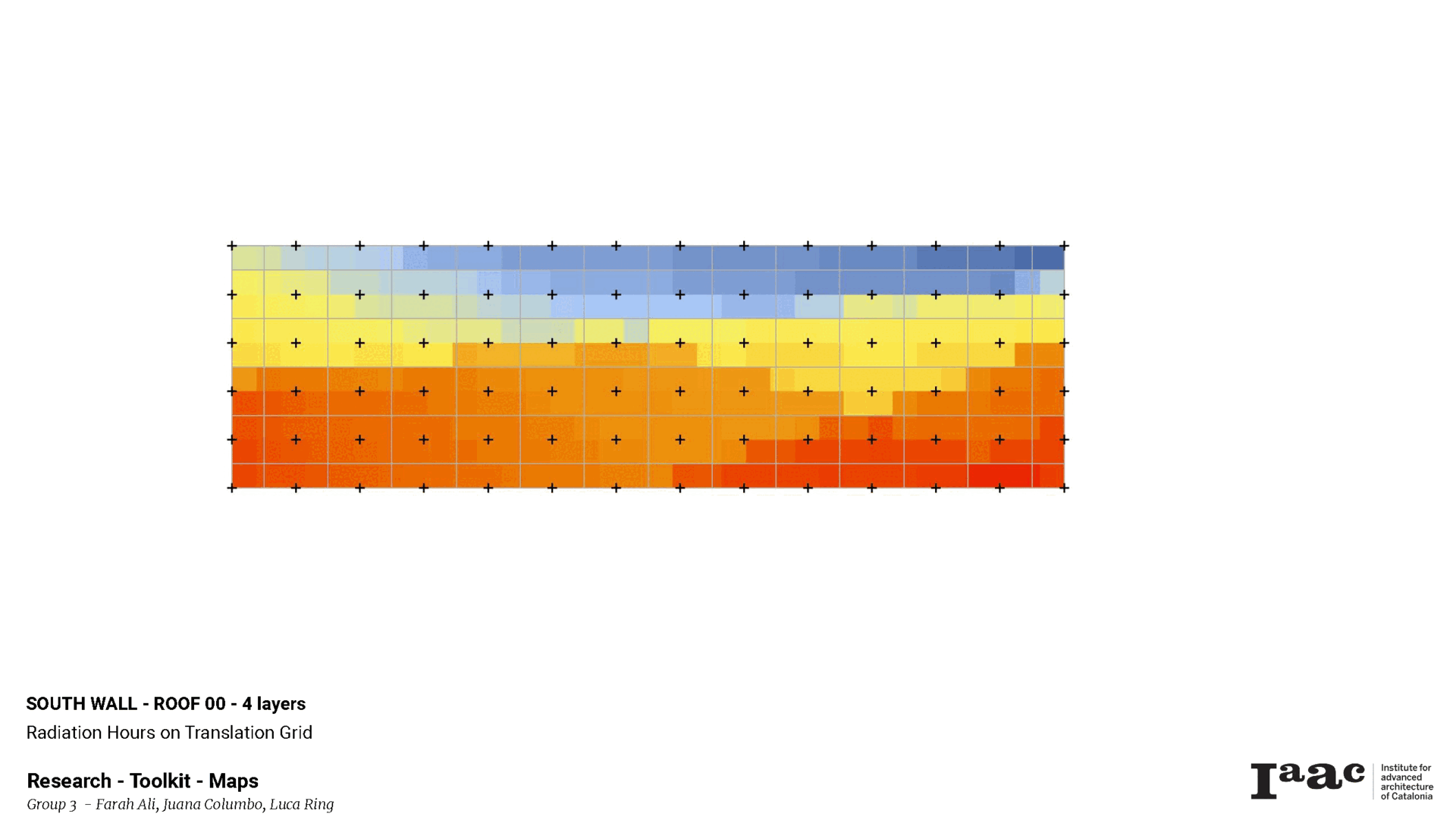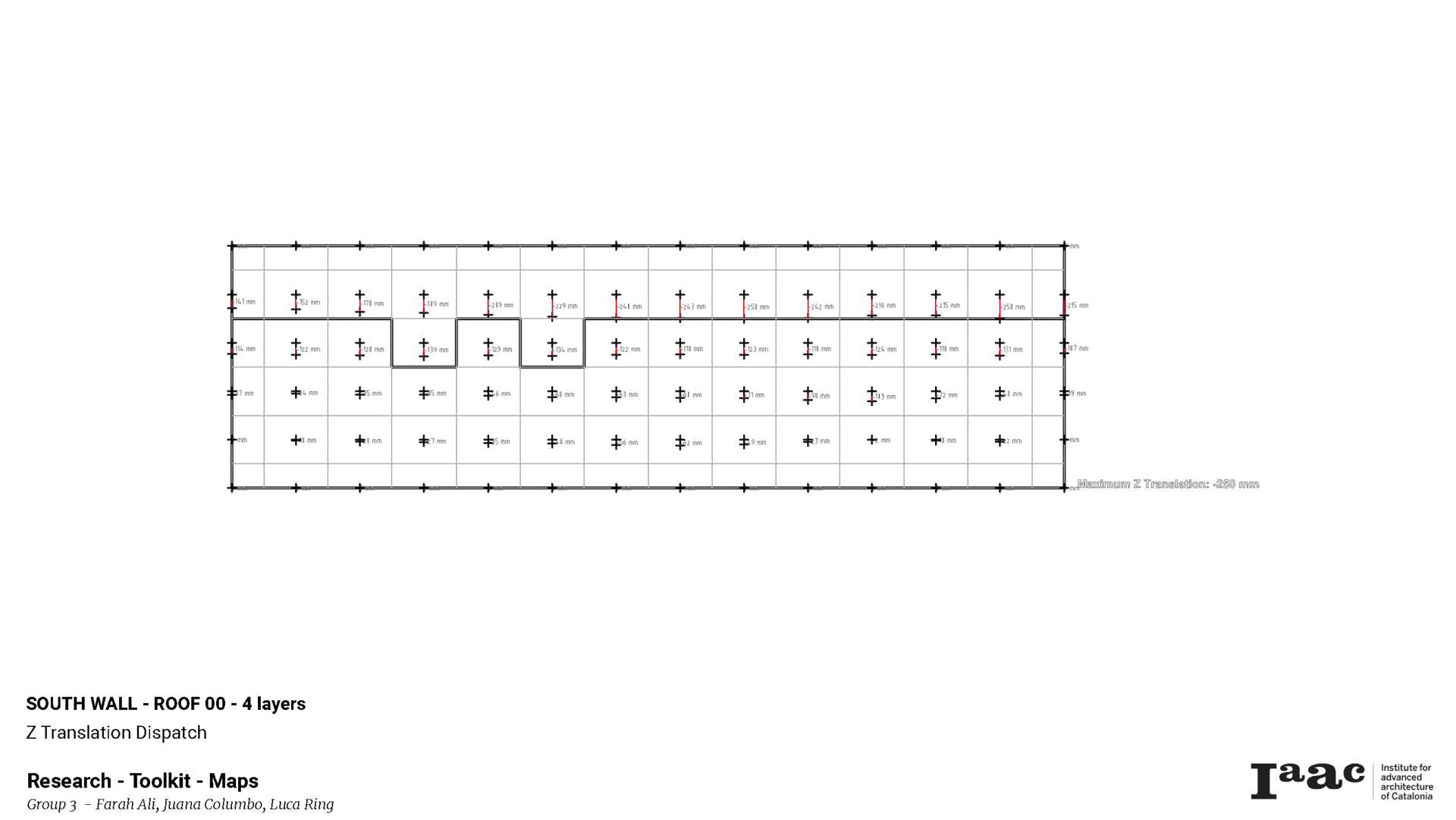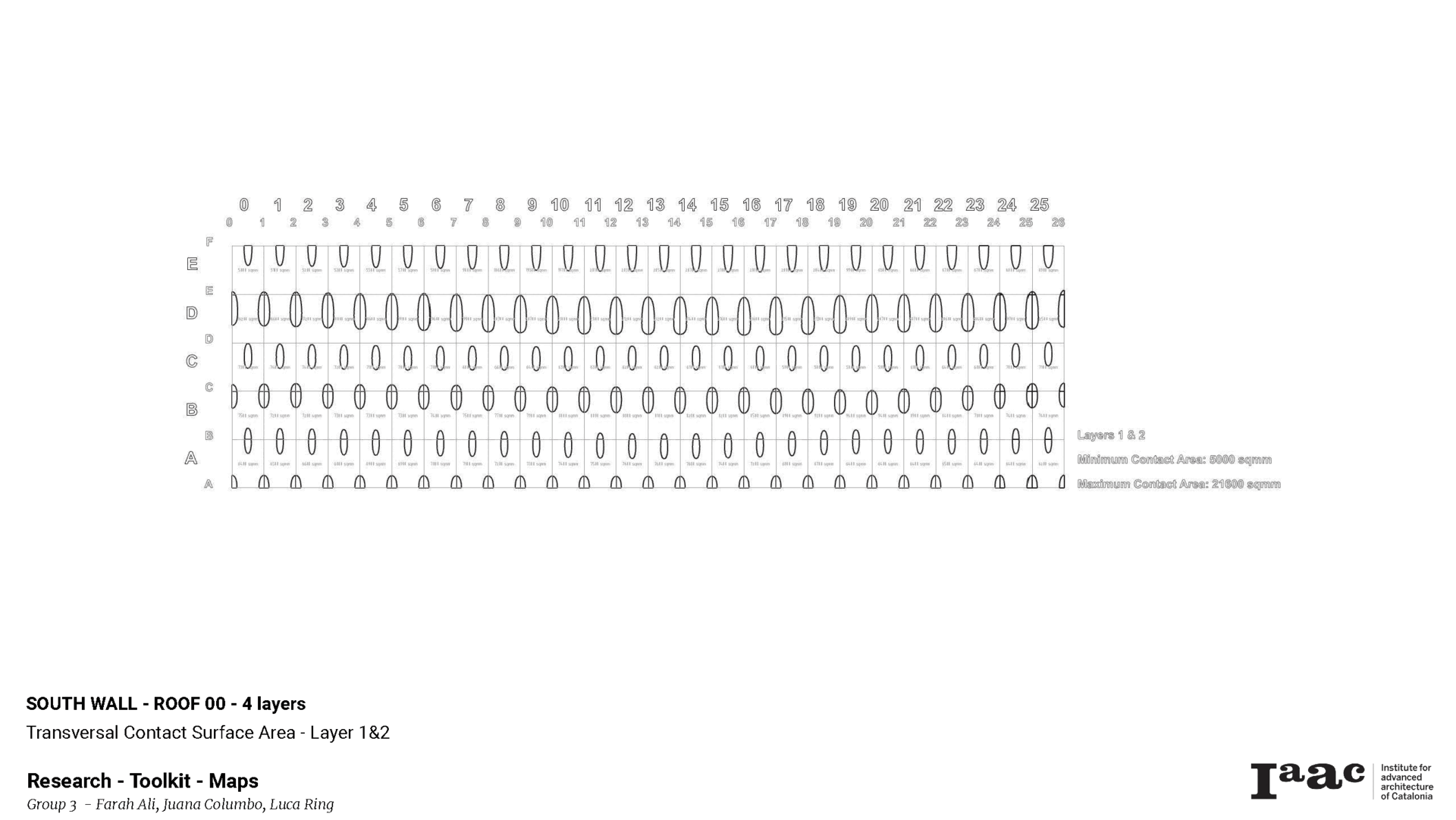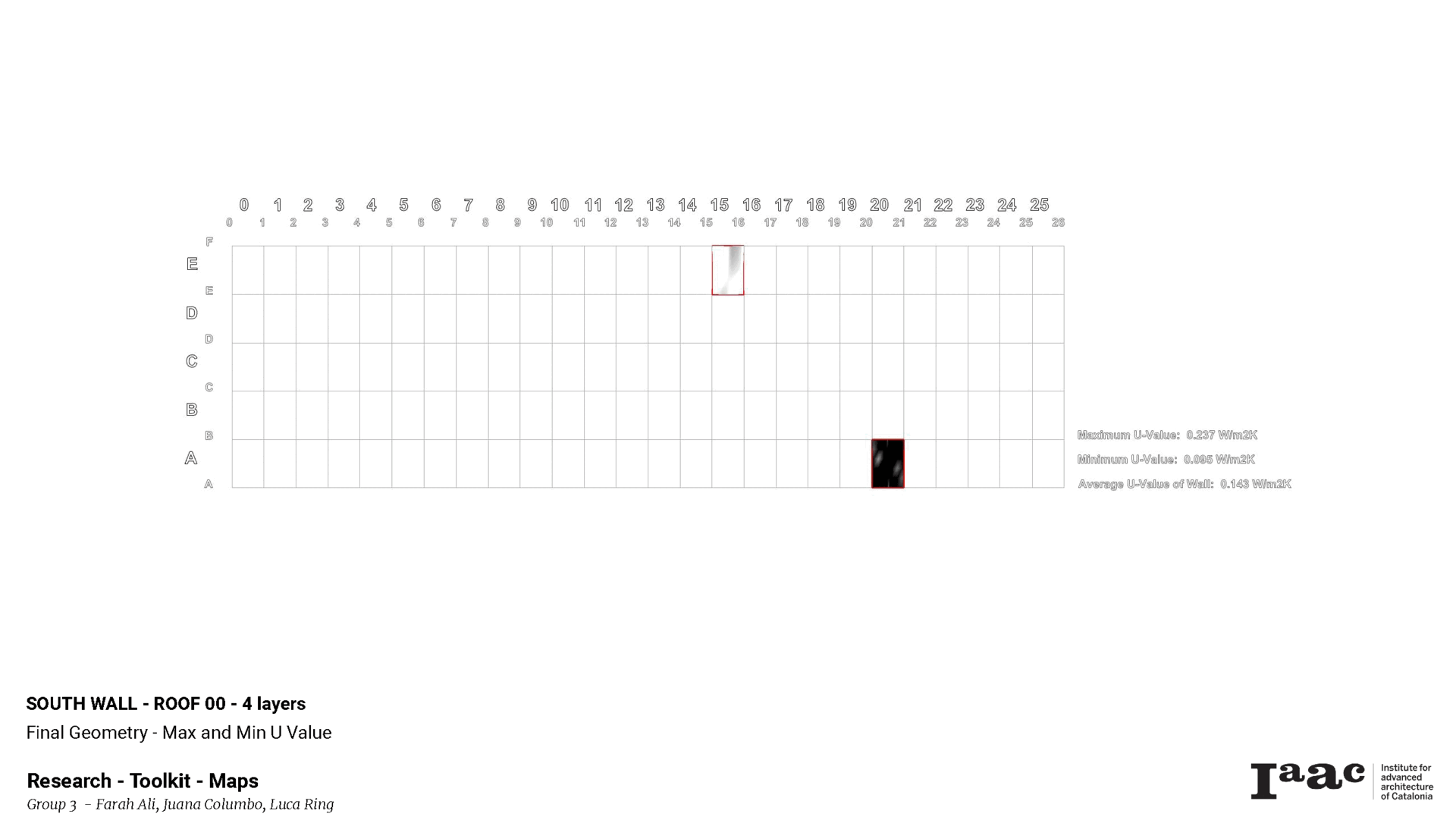
The toolkit-generated wall has an average U-Value of 0.14 W/m2K for the unique parameters & location that were used during the research to produce this sample result.
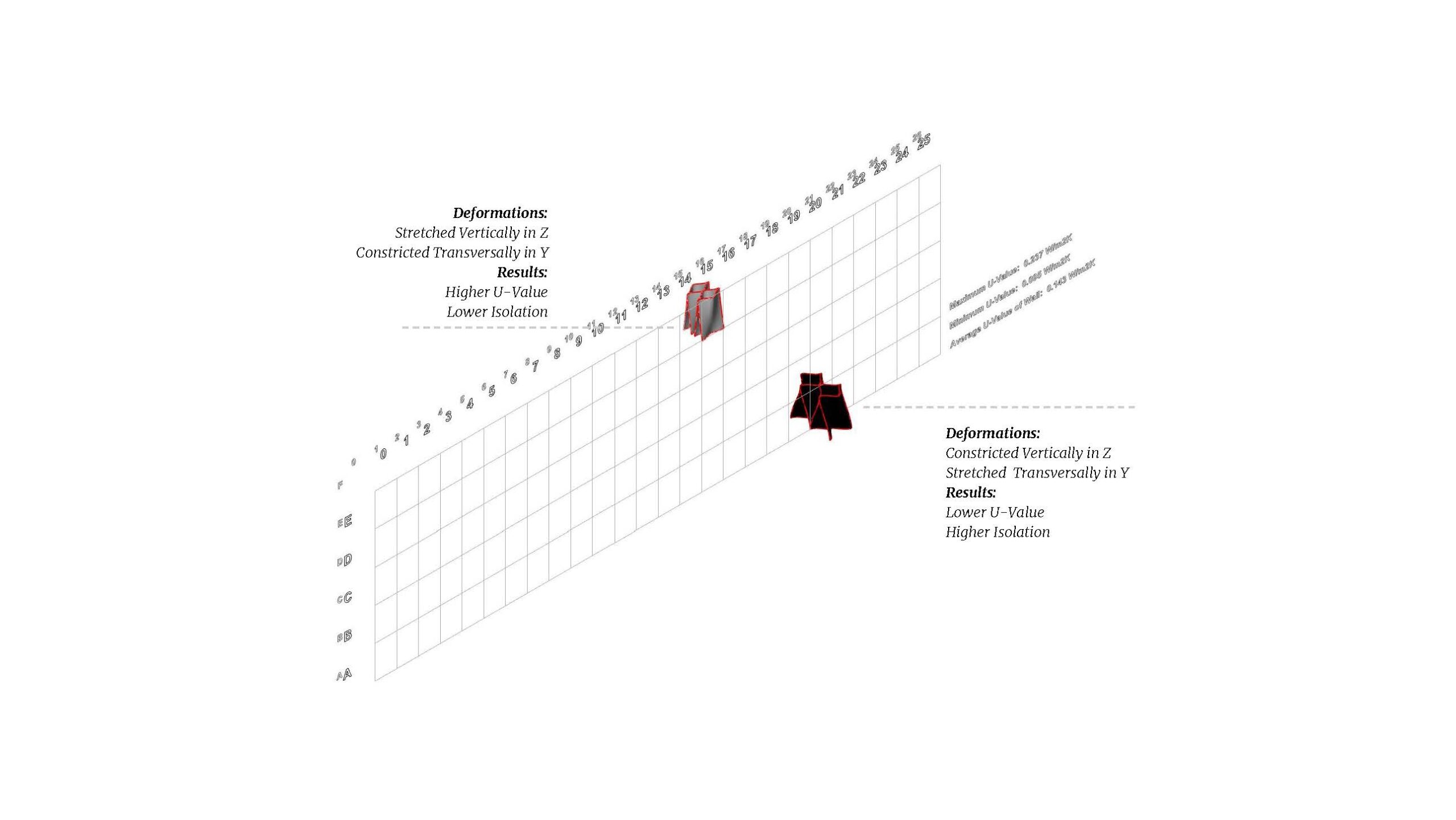
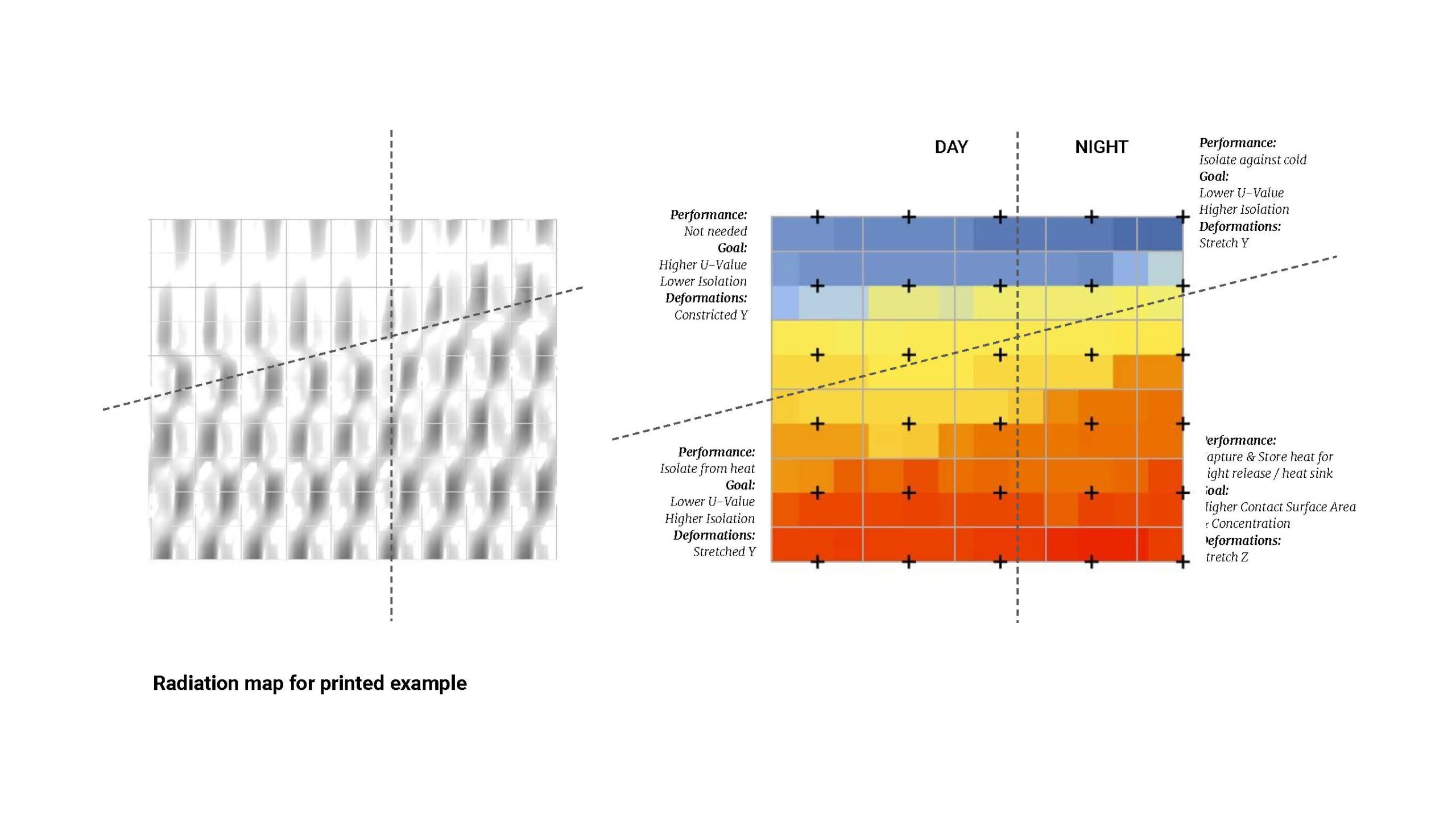
A quick isolation of the portions with the maximum & minimum U-Values further solidifies the previous hypotheses detailing which deformations affect the U-Value and in what way. Stretching in Z & Constricting in Y increases U; inversely, constricting in Z and stretching in Y lowers U.
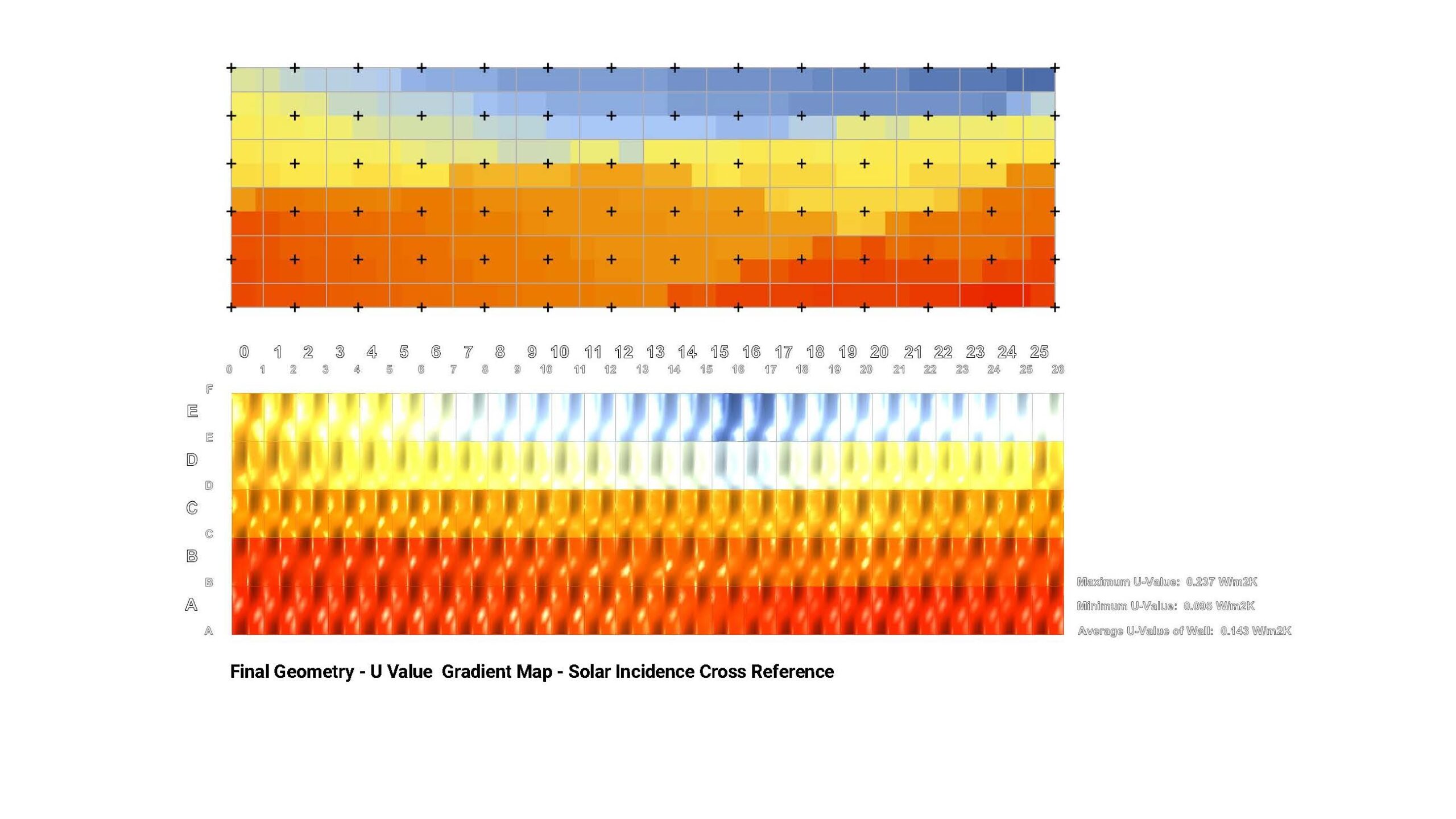
Applying LB colours to the existing U-Value gradient shows the direct correlation between the toolkit deformations’ U-values & the incidence, where the blue tones in the radiation map reflect lower values, the blue reflects lower insulation – or higher U – in the U-value map, and the red tones in the radiation map reflect higher values, reflecting higher insulation – or lower U’s – in the U-value map.
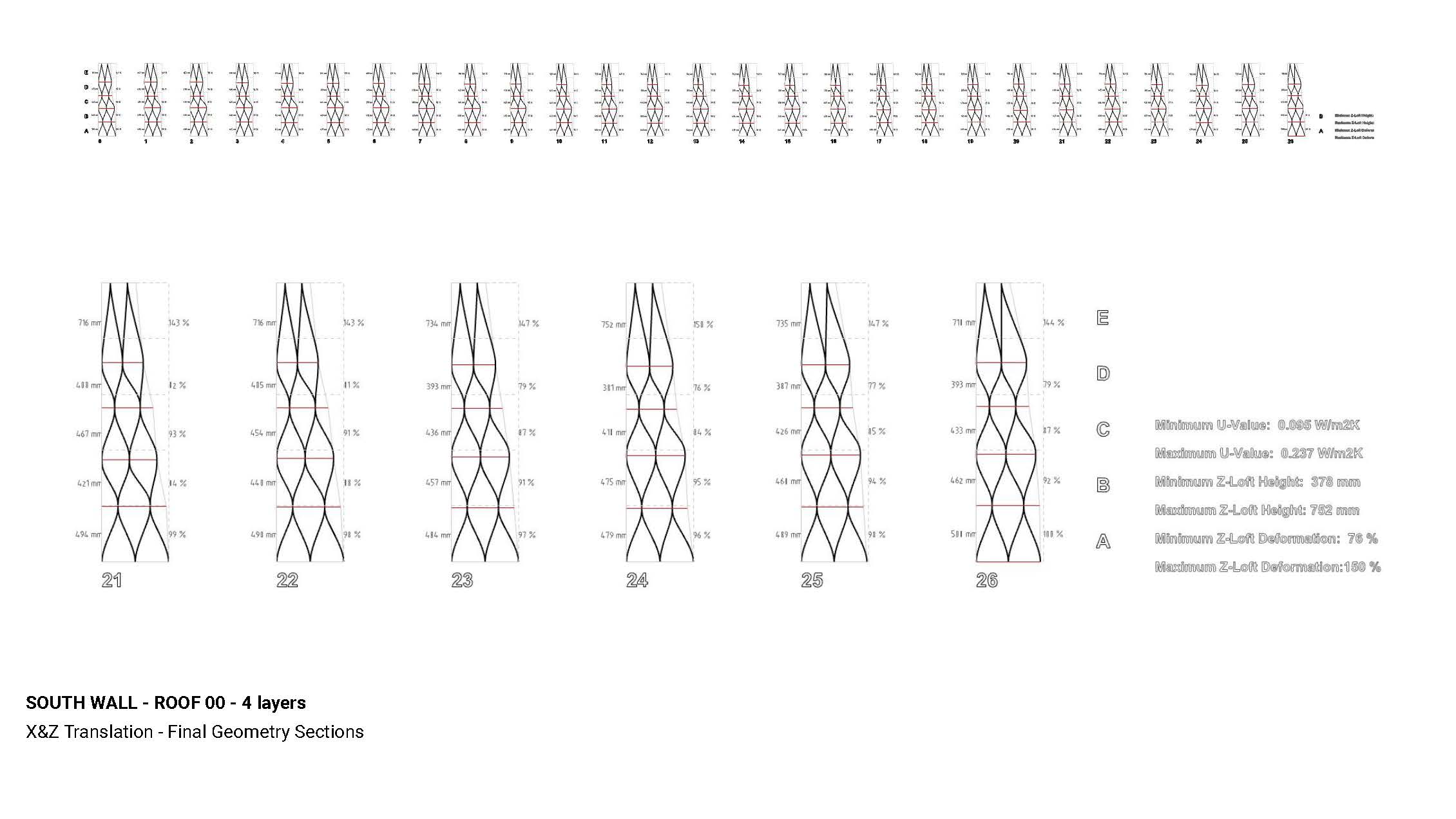
Alongside all previous analysis & data maps produced by the toolkit, the following plans and sections are also produced to map out the deformations.

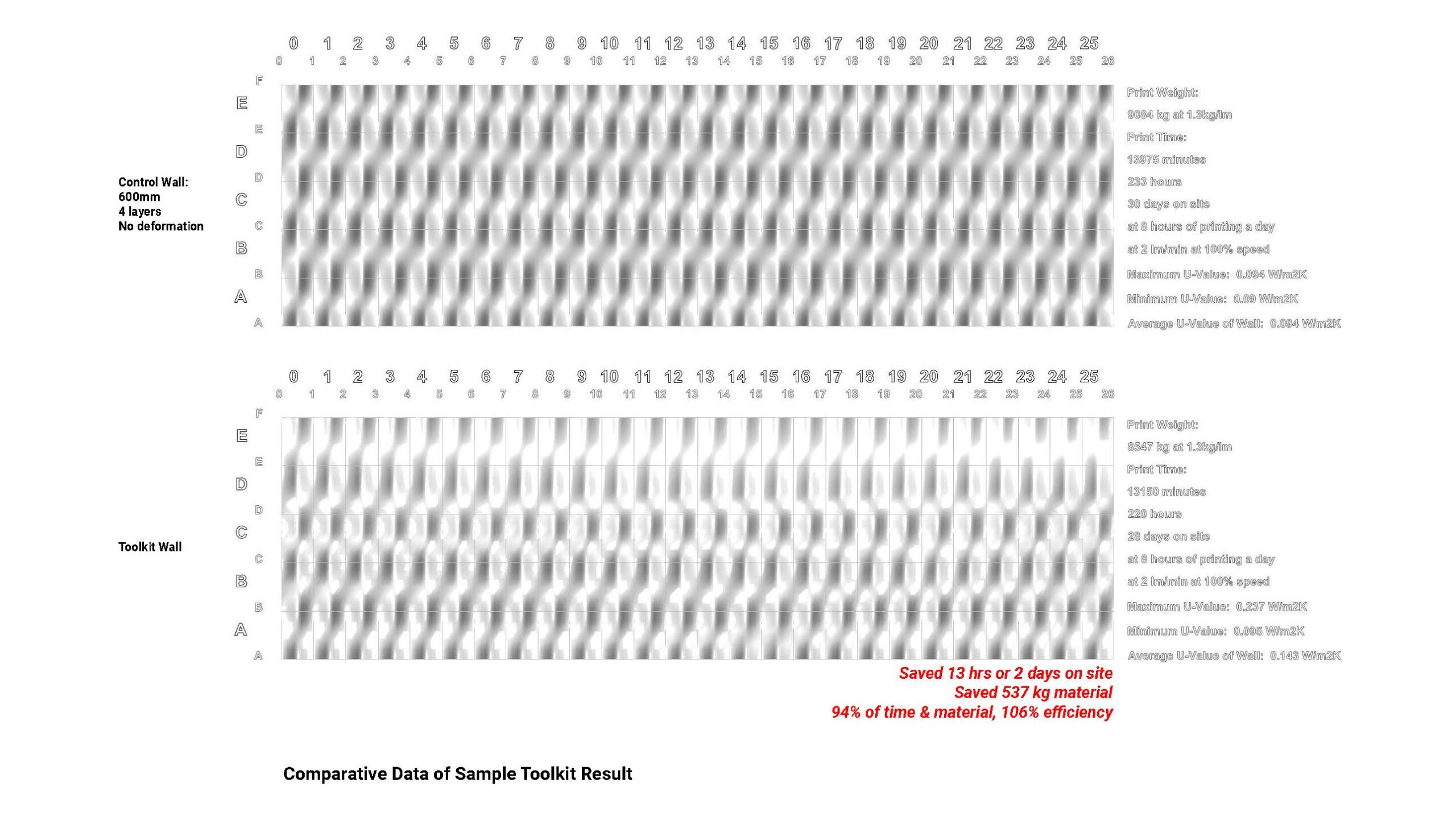
A comparison with a wall with the same base parameters & no applied deformations was conducted to quantify the efficiency of this research’s deformation methodology. Compared to a 600mm 4 layer wall, the toolkit wall is 106% more efficient, saving roughly 2 days of on-site printing & half a ton of material on one wall alone.
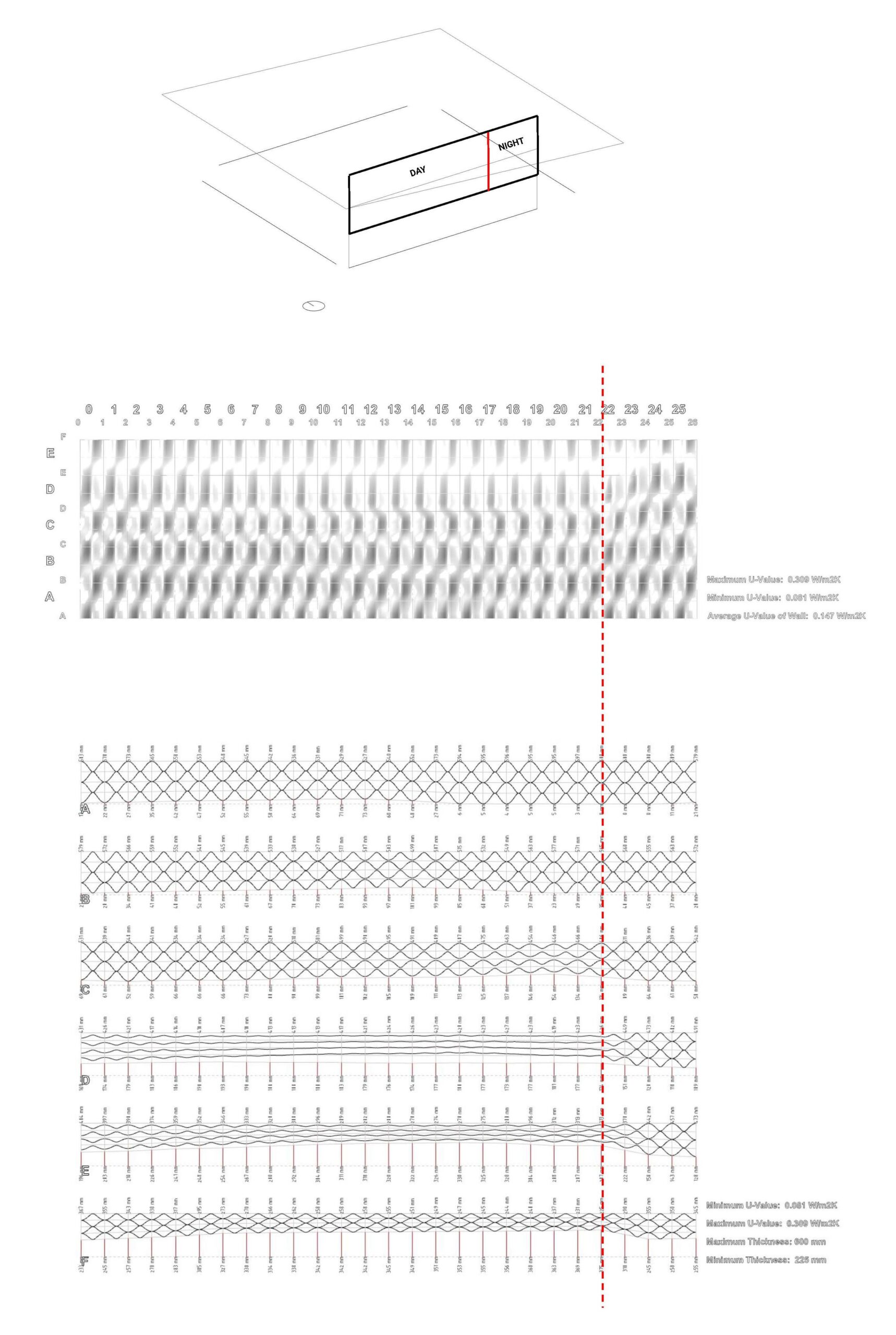
Another feature is the possibility of defining where a change in program happens behind a wall and consequently treating the wall differently according to the time of day the program inhabits, allowing for varying, or even contradicting, thermal performances.
The following graphic showcases the logic of all the steps & analyses taken in the toolkit to arrive at the final geometries, including the quantification of the Contact Surface Area, or Thermal Bridges, necessary for the incorporation into the new proposed U-Value calculation for 3D printed architecture.
1:2 Scale Prototype
This prototype validates the buildability of the toolkit’s physical output, even with extreme transitions in the deformation across the Z and transversal axis.

