Leveraging the Wave Function Collapse Algorithm for Application on Layered Quadrilateral Meshes

Abstract
Procedural Morphologies is a novel computational design workflow in the field of discrete design. It leverages the Wave Function Collapse Algorithm for application on any quadrilateral mesh. Thus a coherent three-dimensional aggregation solution can be generated for any quad mesh using a tile set and heuristic rules. The mesh’s faces are offset to create twisted boxes. These are populated with the provided tiles using a modified “Monoceros” solver. The script can operate on meshes with highly complex topologies and therefore opens new possibilities for discrete design applications on freeform geometries.
Introduction
The advancements in computational design over recent years have marked a significant shift in the fields of architecture, design, and fabrication. An explosion of complex geometries, fuelled by evolving digital tools and leaps in digital fabrication technologies, has transcended traditional constraints and opened doors to unimaginable possibilities. But as is the nature of progress, every solution introduces new problems.
As the complexity in design escalates, it has become increasingly challenging to manage the diverse geometric topologies that emerge. The intricacy of relationships between individual components becomes non-standard, unpredictable and demands tools that are capable of interpreting and manipulating these complexities.

Procedural & Discrete Design
Within computational design, procedural and discrete design methods have offered a way to automate complex design workflows. These methods facilitate the rapid iteration of complex geometries and topologies. While they operate on separate principles, the intersection of procedural and discrete design offers a fertile ground for exploration and innovation.
Discrete design focuses on individual parts and their connections to create a cohesive whole. This makes it more suitable for fabrication as the process can begin with a module that’s already manufacturable. The design method in this thesis explores a combinatorial approach, using procedural methods on discrete assemblies.
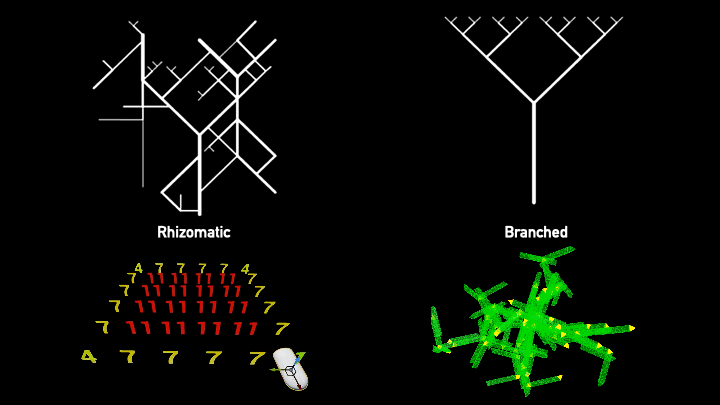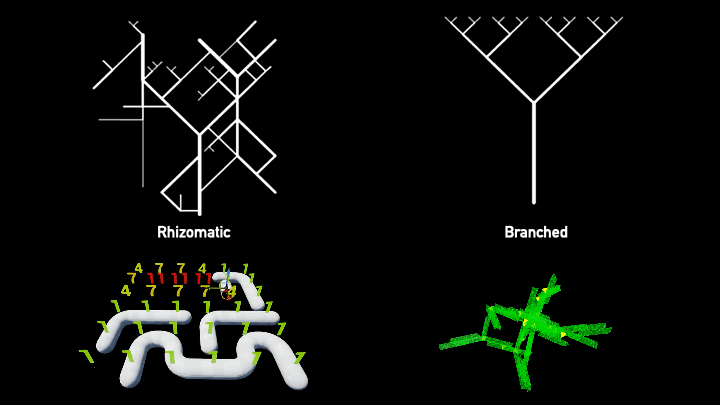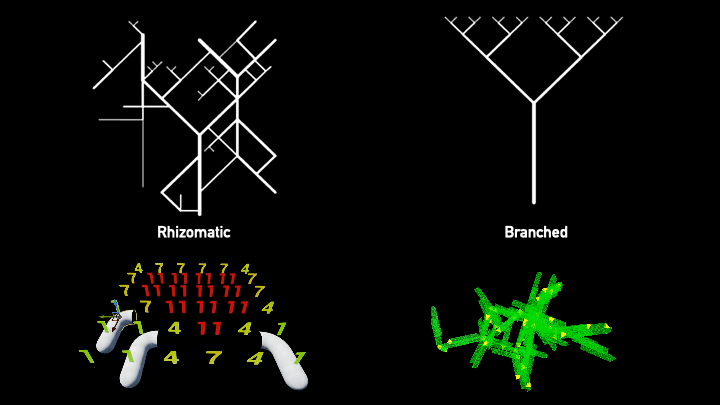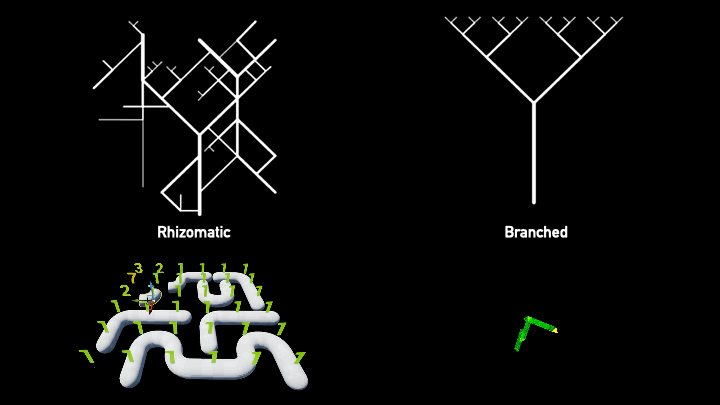
Constraint Modeling vs Growing Algorithms
Discrete design methodologies primarily revolve around two combinatorial tools: constraint modeling, such as Monoceros using the Wave Function Collapse (WFC), and growing algorithms like Wasp and Assembler. Each uses a modular 3D tile set, heuristics, and rules to shape the design.
WFC operates on the principle of logic-based aggregation. The algorithm treats each space as a slot that must be filled, similar to solving a Sudoku puzzle, respecting the constraints of the given rules. On the other hand, growing algorithms work sequentially, beginning with a starting point and branching off from there.
For our purpose, we focus on WFC due to its compatibility with irregular meshes, where logic aggregation makes more sense. Maintaining the topology becomes significantly more straightforward with this approach.

Wave Function Collapse Algorithm (WFC)
WFC has found its applications predominantly in game level design and architecture where regular grid systems and voxels are common. The algorithm generates intricate and realistic environments by starting with a small seed pattern and then iteratively expanding and “collapsing” the probabilities of neighboring elements until a complete structure is formed.
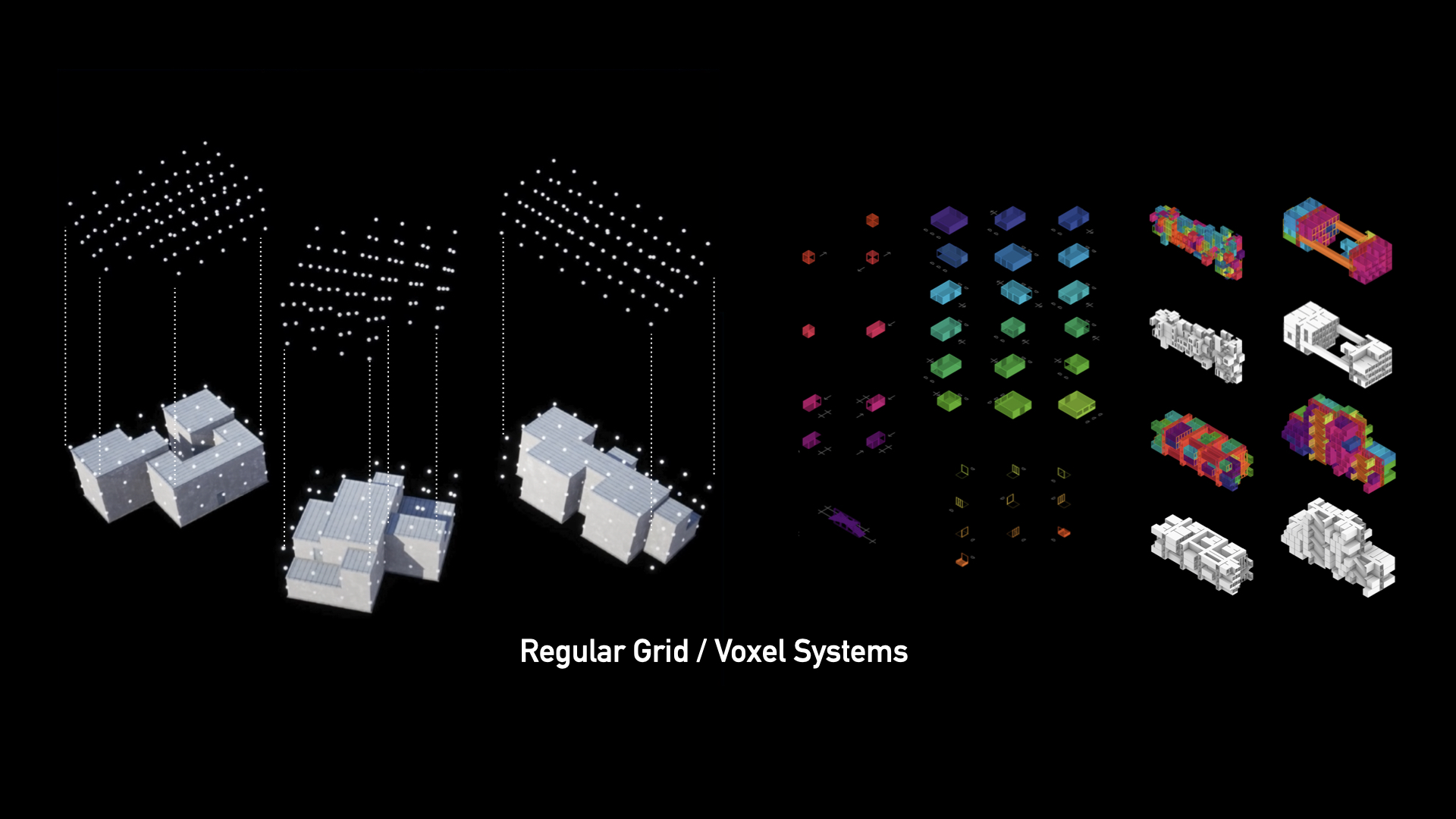
Limitation of Current WFC Tools
The existing WFC tools are restricted to regular grids or voxel systems, not fully exploiting their potential in the realm of computational design. They are largely incapable of handling geometries with complex topologies, making them unfit for a wide range of applications.

medieval-plans-seen-from-above (2) Kangaroo Shell Structure: parametrichouse.com/kangaroo-shell-structure/ (3) Character Topology: skif3d-eng.blogspot.com
Possible Complex Topology Applications
The ability to apply WFC to complex topologies can bring about a radical transformation in the design of complex city grids, shell structures, character designs, freeform product designs, and massive superstructures, among other things.

WFC on a simple 2D tile set
To demonstrate the working of WFC, consider a simple tile set with water, coast, and land. We establish simple rules for their placement relative to each other. We can begin with a 5×5 grid and follow the process of propagation. As we increase the complexity of the tile set and rules, the complexity of the output also increases.

Morphology #1: Seifert Surface Space Station
The first case study explores the design of a space station using a Seifert surface, which is orientable, two-sided, and has low curvature. The singularity points of the Seifert surface are utilized to draw edge loops, which then help create patches for mesh preparation. This setup necessitates a large tile set, one of the complexities when dealing with the WFC. However, with procedural post-processing, many connectors can be designed for all possible outcomes, allowing for rich, complex structures.

Morphology #2: Gyroid Lamp
The second case study deals with a more domestic application —a lamp— using a gyroid as the base geometry. Like the Seifert surface, the gyroid has low curvature and is two-sided. The goal is to use polypropylene sheets to create a laser-cut lamp with three layers. This project employs a simpler tile set, providing a contrast to the first case study and demonstrating the versatility of the WFC.
Future Implications
While these applications have shown promising results, the limitations of scripting in Grasshopper have been reached. Future development is planned in creating a standalone plugin that will be better equipped to handle the complexities of the WFC, leveraging advancements like multi-threading and offering a more specialized solver.
The plugin will have additional features such as visualizing the propagation process and offering more constraint options, making it a more powerful tool for computational design. This will open up new possibilities for designers, enabling them to use the WFC on a broader scale and with more complex topologies.
In conclusion, the adaptation of the Wave Function Collapse Algorithm for application on any quadrilateral mesh presents a significant leap forward in the field of computational design. By expanding the potential use cases for WFC, we are set to open a new frontier in procedural morphologies, bringing more complex and intricate designs within our reach.

